CURSO SOBRE EL CRIPTOSISTEMA DE CURVAS ELÍPTICAS
Para el desarrollo correcto de este curso es necesario que se tengan unos conocimientos mínimos de matemáticas de ingeniería. Además, para el buen funcionamiento de este curso, es recomendable disponer de la versión 10 de Maple o superior para que pueda ser interactivo.
IMPORTANTE: Para que la navegación sea más cómoda, debes quitar las restricciones para el código autoejecutable. ¿Cómo?
Consejos de navegación: Se recomienda estudiar el capítulo 2 para comprender el funcionamiento de la librería que se va a utilizar en los ejercicios propuestos. Además es importante estudiar los capítulos 4 y 5 antes de comenzar la lección 6, porque suponen la base de este último. Sin embargo, el usuario de este curso puede navegar a su gusto por los diferentes capítulos que lo componen. Al hacer clic en los hiperenlaces, se recomienda abrir las hojas de trabajo en una pestaña nueva para facilitar la navegación. ¿Cómo?
Cuando aparezca el icono ![]() podremos pinchar sobre él para ampliar la información que estamos tratando. En unas ocasiones nos dirigirá a otras secciones dentro del curso y en otras, nos enviará a enlaces externos, por lo que es recomendable que dispongamos de conexión a internet.
podremos pinchar sobre él para ampliar la información que estamos tratando. En unas ocasiones nos dirigirá a otras secciones dentro del curso y en otras, nos enviará a enlaces externos, por lo que es recomendable que dispongamos de conexión a internet.
1. Presentación del Curso sobre el Criptosistema de Curvas Elípticas
1.1 Objetivo
El curso pretende ser una herramienta interactiva para profundizar en los aspectos tanto teóricos como prácticos del Criptosistema de Curvas Elípticas. Se dirige a cualquier persona que esté interesada en el conocimiento de este Criptosistema, especialmente si son estudiantes de ingeniería con conocimientos previos en el ámbito de la criptografía.
En la actualidad, el Criptosistema de Curvas Elípticas está adquiriendo importancia y protagonismo en el cifrado de mensajes. Sin embargo, la información sobre este criptosistema es escasa y difícil de encontrar.
La criptografía es la parte de la criptología que se ocupa de las técnicas que alteran las representaciones lingüísticas de los mensajes para ocultarlos a terceros, ajenos al emisor y el receptor, que puedan interceptar esos mensajes. De este modo, su finalidad es conseguir la confidencialidad de los mensajes. ![]()
Para el desarrollo del curso se ha elegido el software matemático Maple, que nos permite realizar operaciones en aritmética modular, además de poder manipular de un modo algebráico, variables y símbolos. También podremos operar con vectores y matrices, además de poder visualizar resultados con gráficas en 2 y 3 dimensiones. A todo esto hay que añadir que contiene una amplia biblioteca con más de 3000 funciones matemáticas agrupadas por objetivos y que trabajaremos con un lenguaje de programación de alto nivel.
Es necesario que los usuarios tengan unos conocimientos básicos de la herramienta Maple. De no ser así, se puede consultar el siguiente tutorial para familiarizarse con la herramienta.
1.2 Breve recorrido histórico
El desarrollo de las tecnologías de la Información y el uso masivo de las comunicaciones digitales han incrementado los problemas de seguridad. Por ello, la criptografía se ha centrado en el desarrollo de algoritmos, protocolos criptográficos y sistemas encargados de proteger la información y dotar de seguridad a las comunicaciones y a las entidades que se comunican, aprovechando las técnicas matemáticas como herramientas para conseguir estos objetivos. ![]() Dentro de los métodos de cifrado, podemos distinguir el cifrado simétrico o de clave privada y el de clave pública o asimétrico.
Dentro de los métodos de cifrado, podemos distinguir el cifrado simétrico o de clave privada y el de clave pública o asimétrico.
La criptografía simétrica es una técnica milenaria de cifrado que consiste en cifrar y descifrar mensajes por medio de la misma clave. En este caso, el emisor y el receptor deben ponerse de acuerdo en la clave que van a utilizar. Uno de sus principales inconvenientes es el número de claves que necesita, ya que, en un grupo de n personas sería necesario un número de claves del orden de ![]() , para que cada pareja de personas pueda comunicarse en privado. Por tanto, este sistema quedaría acotado a grupos reducidos de personas.
, para que cada pareja de personas pueda comunicarse en privado. Por tanto, este sistema quedaría acotado a grupos reducidos de personas. ![]() Sin embargo, el principal problema es el de la distribución de claves. La distribución de claves requiere que o bien cada pareja de personas acuerde una clave de algún modo, o bien se utilice un centro de distribución de claves. Esta segunda vía, según Whitfield Diffie, uno de los descubridores del cifrado de clave pública, atenta contra la esencia misma de la Criptología: la habilidad de mantener una garantía total de confidencialidad en las comunicaciones.
Sin embargo, el principal problema es el de la distribución de claves. La distribución de claves requiere que o bien cada pareja de personas acuerde una clave de algún modo, o bien se utilice un centro de distribución de claves. Esta segunda vía, según Whitfield Diffie, uno de los descubridores del cifrado de clave pública, atenta contra la esencia misma de la Criptología: la habilidad de mantener una garantía total de confidencialidad en las comunicaciones. ![]()

Whitfield DIffie
Por otra parte contamos desde 1977 con la criptografía asimétrica o de clave pública, creada por Whitfield Diffie y Martin Hellman. Este método emplea un par de claves para el envío de mensajes, de manera que cada usuario A tendrá una clave pública que podrá entregar a cualquier persona, y una clave privada que deberá guardar sin que nadie tenga acceso a ella. Cualquier otro usuario B podrá enviar mensajes a A cifrándolos con la clave pública de A y éste los descifra con su clave privada. De este modo se consiguen varios objetivos:
1. Garantizar la confidencialidad en el envío de mensajes, evitando así el problema del intercambio de claves que presentaban los sistemas de cifrado simétricos.2. Autenticar la identidad de los emisores.3. Minimizar el número de claves, pues en este sistema sólo serán necesarios n pares de claves por cada n personas que deseen comunicarse entre sí.

Martin Hellman
Algunos ejemplos de protocolos basados en la clave asimétrica son el intercambio de claves de Diffie-Hellman, cifrado RSA, DSA (Digital Signature Algorithm ó algoritmo de firma digital), criptosistema de ElGamal y la criptografía de curva elíptica.
En los esquemas de clave asimétrica, obtener la clave privada a partir de la pública es equivalente a resolver un problema computacionalmente intratable. Entre los problemas de teoría de números cuya intratabilidad forman la base de la seguridad de los criptosistemas podemos citar:
a) La factorización en enteros, esencial para la seguridad del criptosistema RSA y la firma digital.b) El logaritmo discreto para números enteros, básico para la seguridad del criptosistema de ElGamal y esquemas de los criptosistemas de firmas como DSA.c) El logaritmo discreto sobre curvas elípticas, esencial para la seguridad del criptosistema de Curvas Elípticas. ![]()
Actualmente, uno de los criptosistemas más utilizados es el RSA (Rivest, Shamir y Adleman). Se trata de un sistema criptográfico de clave pública desarrollado en 1977 por Ron Rivest, Adi Shamir y Len Adleman. Fue el primer criptosistema de clave pública y puede utilizarse tanto para cifrar como para firmar digitalmente. La seguridad de este algoritmo radica en la dificultad computacional del problema de la factorización de números enteros. Esto es porque los mensajes enviados se representan mediante números enteros y, para descifrar los mensajes sin conocer la clave privada, es necesario factorizar un entero que es el producto de dos números primos grandes elegidos al azar y mantenidos en secreto. En la actualidad estos primos son del orden de ![]() , y se prevé que su tamaño aumente con la capacidad de cálculo de los ordenadores.
, y se prevé que su tamaño aumente con la capacidad de cálculo de los ordenadores.
Ron Rivest |
Adi Shamir |
Len Adleman |
Puesto que la seguridad del cifrado RSA depende de la factorización de un entero, dicha seguridad se ve comprometida por el continuo refinamiento de los algoritmos de factorización. Esto ha llevado al crecimiento del tamaño de la clave hasta los 1024 bits de la actualidad. Este tamaño de clave tiene como consecuencia que se ralenticen ciertas aplicaciones que utilizan RSA, especialmente las realizadas con el comercio electrónico que deben transmitir números muy grandes para las comunicaciones seguras. Además, la computación cuántica podría proporcionar una solución al problema de factorización, así como al problema del logaritmo discreto.
El continuo aumento del tamaño de clave para garantizar la seguridad del criptosistema RSA ha dado pie a que el criptosistema de curvas elípticas haya ido tomando fuerza hasta el día de hoy.
La teoría de curvas elípticas cuenta con más de un siglo de existencia, ya que sus orígenes datan de mediados del siglo XIX. Sin embargo, no es hasta finales de la década de 1980 y principios de la de 1990 cuando comienza su aplicación a la criptología por parte de Neal Koblitz y Victor Miller entre otros. ![]()
![]()
Neal Koblitz |
Victor Miller |
La criptografía de curva elíptica es un criptosistema asimétrico o de clave pública basado en la aritmética de las curvas elípticas. En este caso, los mensajes se representan mediante puntos de la curva. Para obtener el mensaje en claro a partir del mensaje cifrado hay que resolver el problema del logaritmo discreto en curvas elípticas. Los algoritmos conocidos para resolver el problema del logaritmo discreto en curvas elípticas son de complejidad exponencial, a diferencia de los algoritmos para factorizar enteros, que son subexponenciales. Eso hace que para el mismo nivel de seguridad se requieren tamaños de clave más pequeños, por ejemplo que los de RSA, lo que reduce los procesos de cifrado. Este es el principal atractivo de las curvas elípticas.
En el ámbito de la industria, los criptosistemas de curvas elípticas han conseguido estándares (IEEE P1363) y fabricado productos que se están comercializando. Además, NIST y ANSI X9 han establecido como requisitos mínimos de tamaño de clave de 1024 bits para RSA y DSA y de 160 bits para el criptosistema de curva elíptica, por lo que se puede comprobar que el tamaño de las claves varía sustancialmente.
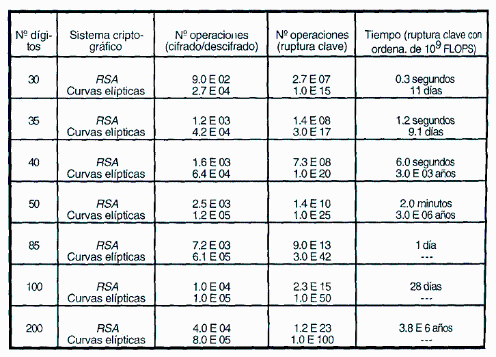
Tabla 1. Esfuerzo computacional para Criptoanálisis de Criptografía de Curvas Elípticas comparado con RSA.
En cuanto a las aplicaciones de las curvas elípticas, desde el 1 de noviembre de 2010 se encuentra en circulación el DNI alemán electrónico (eID card). Este medio de identificación incluye un chip que funciona con tecnología RFID (Radio Frequency IDentification o identificación por radiofrecuencia) que almacena los datos del propietario. Su novedad principal es que emplea la criptografía de curvas elípticas para garantizar la seguridad en las transacciones electrónicas que permita realizar. Para ser más exactos, utilizará curvas de 256 bits, por lo que proporciona un nivel alto de seguridad. ![]()
En España, la Fábrica Nacional de Moneda y Timbre (FNMT-RCM) está trabajando actualmente en el pasaporte electrónico, cuya generación de claves se basa en el criptosistema de curvas elípticas. De este modo se aprovecha que con una longitud de clave más corta se ofrece el mismo nivel de seguridad que con el criptosistema RSA.
1.3 Notas y curiosidades
Como dato histórico se puede encontrar el artículo original de RSA en Rivest, R., Shamir, A., Adleman, L.: A Method for Obtaining Digital Signatures and Public Key Cryptosystems. Communications of the ACM, Vol 21 (2), pp. 120 – 126. 1978. Previamente publicado como una “Memoria Técnica” del MIT en abril de 1977. Publicación inicial del esquema RSA.
Para ampliar información sobre la comparativa del tamaño de las claves de RSA y de Curvas Elípticas, se recomienda Koblitz, N.: Elliptic Curve Cryptosystems, Mathematics of Computation. 48, 1987, pp 203 – 209.
2.1. Carga de la librería CurvasElipt
Para el funcionamiento y utilización de la librería, habrá que abrir el documento en la misma carpeta en la que se encuentre el fichero de la librería y ejecutar el siguiente grupo de funciones:
| > | restart;
libname:= libname,".": with(CurvasElipt); |
2.2. Información sobre las funciones de la librería CurvasElipt
El paquete CurvasElipt contiene las siguientes variables y funciones:
Variable que contiene un alfabeto basado en el ASCII imprimible y que consta de 113 caracteres. Añade al anterior vocales acentuadas (mayúsculas y minúsculas) la letra “ñ” y otros caracteres especiales y signos de puntuación.
Calcula la tira de caracteres que está asociada a un número.
Calcula el equivalente numérico de una tira de caracteres.
Genera la clave pública y la clave privada para trabajar con el Criptosistema ElGamal.
La clave pública será una terna [p, v1, v2], mientras que la clave privada será un par [p, a] que se guardará en una variable que se introduce como parámetro de entrada, siendo p un número primo, v1 una raíz primitiva mod p y v2 = ![]() mod p, donde a es un número entero aleatorio secreto.
mod p, donde a es un número entero aleatorio secreto.
Permite cifrar y descifrar mensajes por medio del Criptosistema ElGamal.
Calcula el logaritmo discreto para un número entero a en ℤp: logb (a)(mod p).La finalidad de esta función es comprobar la fiabilidad de las claves generadas para el Criptosistema ElGamal, en función del tiempo que se tarda en romperlas.
Devuelve una lista con todos los puntos de la curva elíptica. Si se le indica en la llamada, también devuelve una gráfica con los puntos de la lista como efecto colateral.
Calcula el logaritmo discreto para curvas elípticas. Esto quiere decir que trata de encontrar el número k de modo que Q = k • P, siendo Q y P puntos dados de la curva elíptica. La finalidad de esta función es comprobar la fiabilidad de las claves generadas para el Criptosistema de Curvas Elípticas, en función del tiempo que tardan en romperlas.
MúltiploPunto
Multiplica un punto de una curva elíptica por un número entero.
Realiza la suma entre dos puntos de una curva elíptica. Si se indica en la llamada, devuelve como efecto colateral una gráfica en la que dibuja los puntos sumandos, así como el punto suma.
Devuelve una tabla con todas las sumas posibles entre dos puntos de una curva elíptica.
Aplica el algoritmo de Koblitz para obtener un punto de una curva elíptica equivalente a un símbolo que recibe. Se trata de una función auxiliar de la variable TextoPunto.
Devuelve el símbolo asociado a un punto de una curva elíptica.
Devuelve la lista de puntos asociados a una tira de caracteres.
Genera la clave pública y la clave privada para trabajar con el Criptosistema de Curvas Elípticas.
La clave pública será un par [k • base, base], mientras que la clave privada será un par [k, base] que se guardará en una variable que se introduce como parámetro de entrada, siendo base un punto de la curva elíptica y k un número entero aleatorio.
Permite cifrar mensajes por medio del Criptosistema de Curvas Elípticas, generando un criptograma.
Permite descifrar criptogramas por medio del Criptosistema de Curvas Elípticas, generando el mensaje en claro correspondiente.
3.1. Introducción
El criptosistema ElGamal es un criptosistema de clave pública basado en la idea del intercambio de claves de Diffie-Hellman y cuya seguridad se sustenta en el problema matemático del logaritmo discreto para números enteros.
Fue descrito por Taher ElGamal en 1984 y, al no estar bajo ninguna patente, es un algoritmo de uso libre.

Taher ElGamal
Podemos utilizar el algoritmo de ElGamal tanto para generar firmas digitales como para cifrar o descifrar.
En los siguientes apartados trabajaremos en cuerpos finitos ![]() , por lo que será necesario utilizar la aritmética modular. Además, para que los ejercicios sean más visuales transformaremos los mensajes en números, por lo que será necesario calcular su equivalente numérico.
, por lo que será necesario utilizar la aritmética modular. Además, para que los ejercicios sean más visuales transformaremos los mensajes en números, por lo que será necesario calcular su equivalente numérico.
Como en todo criptosistema asimétrico, cada participante tiene una clave pública y otra privada. Para generar las claves:
(a) Se elige un primo p y una raíz primitiva g módulo p, que son ambos públicos.(b) Un usuario A elige un entero a ∈ {1, 2, …, p – 1} aleatoriamente, que mantiene oculto, y genera su clave privada [p, a].(c) A difunde c := ![]() (mod p). Su clave pública es [p, g, c].
(mod p). Su clave pública es [p, g, c].
El cálculo de ![]() (mod p) es rápido gracias al algoritmo de exponenciación modular rápida.
(mod p) es rápido gracias al algoritmo de exponenciación modular rápida.
3.2.1. Ejemplo
Vamos a generar una clave de 3 dígitos utilizando la función GeneraClaveGamal de la librería CurvasElipt. Para ello hay que introducir como parámetros el tamaño de la clave y un nombre para almacenar la clave privada:
| > | pública:=GeneraClaveGamal(3, privada); |
| (3.2.1.1) |
| > | privada; |
| (3.2.1.2) |
A continuación, comprueba los resultados anteriores aplicando las fórmulas comentadas en el apartado anterior:
| > | pública[2]&^privada[2] mod privada[1]; |
| (3.2.1.3) |
Comprobamos que el resultado coincide:
| > | is(%=pública[3]); |
| (3.2.1.4) |
Puedes ejecutar las instrucciones anteriores para realizar tus propias comprobaciones.
Para profundizar más sobre esta función puedes consultarla en su página de ayuda GeneraClaveGamal.
3.2.2. Ejercicios
Utiliza la función GeneraClaveGamal de la librería CurvasElipt para crear claves de 5, 10 y 15 dígitos:
| > |
| > |
| > |
A continuación, comprueba los resultados anteriores aplicando las fórmulas comentadas en el apartado anterior:
| > |
| > |
| > |
Supongamos un usuario A, que dispone de un par de claves (pública y privada) de ElGamal. Cuando otro usuario, B, quiere comunicarse con A, obtiene el valor numérico M del mensaje a enviar y realiza el siguiente proceso:
(a) B consulta la clave pública de A, [p, g, c].(b) B elige un entero b ∈ {1, 2, …, p – 1} aleatorio y envía el par (![]() ,
, ![]() ) := [
) := [![]() , M
, M![]() ] ∈ ℤp* × ℤp*.
] ∈ ℤp* × ℤp*.
El usuario A descifra el mensaje (![]() ,
, ![]() ) del siguiente modo:
) del siguiente modo:
• Calcula ![]() (mod p). • Recupera M calculando d(y) :=
(mod p). • Recupera M calculando d(y) := ![]() •
• ![]() ∈ ℤp*.
∈ ℤp*.
Nota: todas las potencias módulo p se pueden calcular con el Algoritmo de Exponenciación Modular Rápida.
3.3.1. Ejemplo
Vamos a generar una clave con la que poder cifrar y descifrar un mensaje:
En primer lugar, generamos la clave:
| > | clavep:=GeneraClaveGamal(4,priv); |
| (3.3.1.1) |
A continuación, utilizamos la función ElGamal para cifrar el mensaje por medio de este criptosistema. A esta función tenemos que indicarle el mensaje, el alfabeto sobre el que vamos a cifrar y la clave pública:
| > | men:="PATATA"; |
| (3.3.1.2) |
| > | cript:=ElGamal(men,castellano,clavep); |
| (3.3.1.3) |
Por último, utilizamos la función ElGamal para descifrar el criptograma anterior. Para ello tendremos que indicarle el criptograma, el alfabeto sobre el que vamos a decodificar y la clave privada:
| > | ElGamal(cript,castellano,priv); |
| (3.3.1.4) |
3.3.2. Ejercicios
Supón dos usuarios, Alicia y Bob, que quieren enviarse mensajes de modo seguro. Sigue el esquema anteriormente explicado, crea un mensaje de texto y cífralo para que Alicia se lo envíe a Bob. Una vez que Bob lo haya recibido, desencriptalo para comprobar que el resultado es correcto. Se recomienda la utilización de la función para cifrar y descifrar ElGamal.
| > |
| > |
| > |
3.4. Elementos del Criptosistema ElGamal
Los elementos del criptosistema ElGamal son:
Alfabetos fuente y código: := ℬ := ![]() donde p es un número primo. Conjunto de claves: := {K = [p, g,
donde p es un número primo. Conjunto de claves: := {K = [p, g, ![]() , a]× ℤ ×
, a]× ℤ × ![]() * ×
* × ![]() * ×
* × ![]() * | p es primo, g raíz primitiva mod p}
* | p es primo, g raíz primitiva mod p}
La terna = [p, g, ![]() ] es la parte pública de la clave, mientras que a es la parte privada.
] es la parte pública de la clave, mientras que a es la parte privada.
Familia de funciones de cifrado: ![]() (x) := (
(x) := (![]() ,
, ![]()
![]() ) (mod p), para todo x ∈
) (mod p), para todo x ∈ ![]() .
.
3.4.1. Ejemplo
Vamos a calcular el tamaño de bloque para ℤ123456789059 cifrando con el alfabeto castellano de la librería CurvasElipt:
| > | p:=123456789059; |
| (3.4.1.1) |
A continuación establecemos el tamaño del alfabeto:
| > | r:=length(castellano); |
| (3.4.1.2) |
Calculamos el tamaño de bloque:
| > | tam:=floor(log[r](p*(r-1)+r)-1); |
| (3.4.1.3) |
Comprobamos que el tamaño de bloque es válido obteniendo el mayor equivalente numérico de un bloque de 5 símbolos:
| > | castellano[113]; |
| (3.4.1.4) |
| > | MensajeNumérico("€€€€€", castellano); |
| (3.4.1.5) |
| > | is(%<p); |
| (3.4.1.6) |
El tamaño de bloque varía en función de los tamaños de p y r. Cuanto mayor sea el tamaño del alfabeto, más grande tendrá que ser el tamaño de p para que pueda aumentar el tamaño de bloque.
3.4.2. Ejercicios
Decide cuál es la lóngitud máxima en la que se se deben partir los bloques de un mensaje para que los mensajes se representen como un elemento de ℤ67 de modo único. Utiliza como alfabeto [A, E, N, O, P, S]:
| > |
| > |
| > |
Para atacar ElGamal, el criptoanalista tiene varias opciones:
• Hallar la clave privada a tal que c = ![]() (mod p) a partir de la clave pública [p, g, c]. Es decir, calcular el logaritmo discreto de c en la base g módulo p. Sin embargo, el cálculo del logaritmo discreto es muy costoso, sobre todo cuando los factores primos de p – 1 son grandes (al menos 20 dígitos). Los mejores algoritmos conocidos tienen complejidad subexponencial.
(mod p) a partir de la clave pública [p, g, c]. Es decir, calcular el logaritmo discreto de c en la base g módulo p. Sin embargo, el cálculo del logaritmo discreto es muy costoso, sobre todo cuando los factores primos de p – 1 son grandes (al menos 20 dígitos). Los mejores algoritmos conocidos tienen complejidad subexponencial.
• Otra posibilidad sería obtener un método que permita obtener ![]() a partir de
a partir de ![]() y
y ![]() . Por el momento, no se conoce ninguna estrategia al respecto a menos que se utilice el logaritmo discreto.
. Por el momento, no se conoce ninguna estrategia al respecto a menos que se utilice el logaritmo discreto.
• Intentar la fuerza bruta: para cada entero del rango 1 ≤ a < p, hay que calcular ![]() (mod p) y ver si ese valor es c. Esto obliga a considerar todos los enteros entre 1 y p – 1, lo cual es muy costoso cuando p es grande.
(mod p) y ver si ese valor es c. Esto obliga a considerar todos los enteros entre 1 y p – 1, lo cual es muy costoso cuando p es grande.
En definitiva, el criptosistema ElGamal basa su seguridad en la conjetura de que el cálculo del logaritmo discreto no es un problema de clase P.
3.5.1. Ejemplo
Vamos a realizar el criptoanálisis de una clave de ElGamal de 3 dígitos y a calcular el tiempo que tarda en romperse la clave:
En primer lugar generamos la clave de 3 dígitos:
| > | clave:=GeneraClaveGamal(3, privada); |
| (3.5.1.1) |
Tomamos el tiempo inicial y aplicamos la función LogaritmoDiscreto con la clave generada:
| > | t:=time(); |
| (3.5.1.2) |
| > | resul:=LogaritmoDiscreto(clave[2],clave[1],clave[3]); |
| (3.5.1.3) |
Mostramos el tiempo que ha tardado el criptoanálisis:
| > | time()-t; |
| (3.5.1.4) |
Comprobamos que el resultado del criptoanálisis es correcto:
| > | is(resul=privada[2]); |
| (3.5.1.5) |
3.5.2. Ejercicios
Genera claves de ElGamal de 5, 7 y 9 dígitos. A continuación realiza el criptoanálisis de la clave con la función LogaritmoDiscreto, evaluando los tiempos de ejecución mediante la función time de Maple.
| > |
| > |
| > |
4.1. Introducción
Aunque la teoría de curvas elípticas tiene más de un siglo de existencia, es a partir de los años 80, principios de los 90, cuando comienza su aplicación a la criptología de la mano de matemáticos entre los que cabe citar a A. Atkin, H. Lenstra y N. Koblitz.
Arthur Oliver Lonsdale Atkin |
Hendrik Lenstra |
Neal Koblitz |
Las curvas elípticas dan lugar a un criptosistema de clave pública basado en el problema del logaritmo discreto en curvas elípticas. En las siguientes secciones se presentan las ideas y resultados básicos de este criptosistema. ![]()
![]()
De un modo muy general, el criptosistema de curvas elípticas tiene el siguiente esquema:
1. El emisor presenta el texto en claro m mediante un punto Pm de una curva elíptica E. 2. Posteriormente, cifra el punto Pm obteniendo otro punto de la curva P´m es decir, c (Pm) = P´m donde c es la función de cifrado. 3. El receptor descifra el criptograma mediante la función inversa de c, llamémosla d, obteniendo Pm = d (P´m ), y transforma el punto en texto en claro.
Nota: Trabajaremos con curvas definidas sobre un cuerpo de escalares que puede ser = ℝ, ℚ, ℤp con p número primo. Si a ∈ diremos que a es un escalar sin distinguir entre números reales, racionales o clases de ℤp . En los diferentes apartados de este curso se utilizarán las clases de ℤp cuyo p sea distinto de 2 y 3. Pero algunos conceptos se ilustrarán gráficamente para curvas definidas sobre ℝ, para comprender su interpretación geométrica.
Sea un cuerpo, llamamos curva elíptica sobre al conjunto de puntos (x, y) ∈ × que verifican la ecuación siguiente:
E(): ![]() =
= ![]() + ax + b
+ ax + b
(donde la cúbica ![]() + ax + b no tiene raíces múltiples), junto con un punto θE, llamado punto del infinito. Si ≠ ℤ2, ℤ3 la ecuación anterior se conoce como forma canónica.
+ ax + b no tiene raíces múltiples), junto con un punto θE, llamado punto del infinito. Si ≠ ℤ2, ℤ3 la ecuación anterior se conoce como forma canónica.
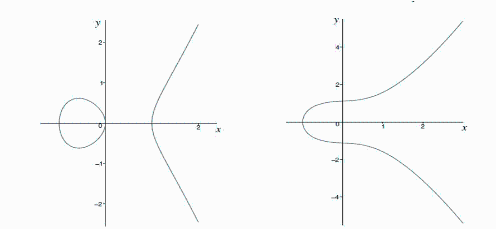
Ejemplos de Curvas Elípticas sobre ℝ.
4.3. Criterio para determinar raíces múltiples
Sea f (x) = ![]() + ax + b un polinomio con coeficientes en :
+ ax + b un polinomio con coeficientes en :
f (x) tiene raíces múltiples si y sólo si ![]() +
+ ![]() = 0 en .
= 0 en .
El número ![]() +
+ ![]() se llama discriminante de la cúbica.
se llama discriminante de la cúbica.
Si una cúbica tiene raíces múltiples, entonces ![]() = f (x) no es una curva elíptica.
= f (x) no es una curva elíptica.
4.3.1. Ejemplo
Vamos a comprobar si la curva ![]() en
en ![]() es una curva elíptica o no:
es una curva elíptica o no:
Para ello vamos a calcular el discriminante de la curva, pero antes representamos los parámetros de la curva mediante variables:
| > | a:=3: b:=1: n:=5: |
| > | discriminante:=(4*a^3 + 27*b^2) mod n; |
| (4.3.1.1) |
| > | is(discriminante=0); |
| (4.3.1.2) |
Tenemos que el discriminante es igual a 0, por lo que la curva tiene raíces múltiples y por tanto, no es una curva elíptica. Podemos comprobarlo:
| > | Factor(x^3+a*x+b) mod n; |
| (4.3.1.3) |
Vemos que la cúbica tiene raíces múltiples en ![]() , x = 2 (raíz doble) y x = 1.
, x = 2 (raíz doble) y x = 1.
Ahora vamos a realizar los mismos cálculos con la curva ![]() en
en ![]() :
:
| > | a:=-4: b:=2: n:=11: |
| > | discriminante:=(4*a^3 + 27*b^2) mod n; |
| (4.3.1.4) |
| > | is(discriminante=0); |
| (4.3.1.5) |
En este caso el discriminante es distinto de 0, por lo que se trata de una curva elíptica.
Vamos a comprobar que se trata de una curva elíptica. Para ello tratamos de descomponer en factores el polinomio:
| > | Factor(x^3+a*x+b) mod n; |
| (4.3.1.6) |
Como no puede descomponerse en factores deducimos que no tiene raíces en ![]() , por lo que confirmamos que se trata de una curva elíptica:
, por lo que confirmamos que se trata de una curva elíptica:
Debido a que se trata de una curva elíptica, vamos a obtener la lista de puntos de la curva. Para ello, en primer lugar vemos cuales son los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to n-1 do cuadrados:={op(cuadrados),i&^2 mod n}; end do; |
| (4.3.1.7) |
Seguidamente calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados. Anteriormente comentamos que no tenía raíces, por lo que ningún valor será igual a 0:
y comprobamos si son cuadrados. Anteriormente comentamos que no tenía raíces, por lo que ningún valor será igual a 0:
| > | for i from 0 to n-1 do
raiz:=[i,(i^3+a*i+b) mod n]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (4.3.1.8) |
En vista de los resultados tenemos que f(7), f(8) y f(10) son cuadrados. Por tanto (7, ± ![]() ) = (7, ±3), (8, ±
) = (7, ±3), (8, ± ![]() ) = (8, ±3) y (10, ±
) = (8, ±3) y (10, ± ![]() ) = (10, ±4) son los únicos puntos de la curva en
) = (10, ±4) son los únicos puntos de la curva en ![]() ×
×![]() . Entonces
. Entonces ![]() en
en ![]() tiene 7 puntos: E(
tiene 7 puntos: E(![]() ) = {(7, 3), (7, 8), (8, 3), (8, 8), (10, 4), (10, 7), θE}
) = {(7, 3), (7, 8), (8, 3), (8, 8), (10, 4), (10, 7), θE}
A continuación, por medio de la función ListarPuntos comprobamos los resultados obteniendo la lista de los puntos de la curva y su representación gráfica:
| > | ListarPuntos(a,b,n,true); |
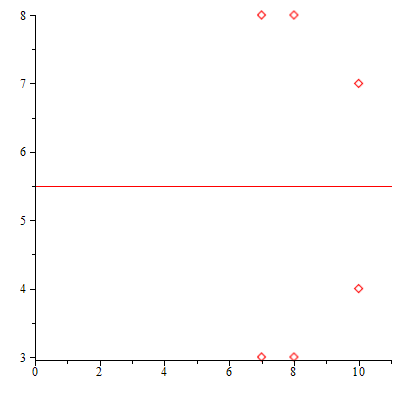 |
|
| (4.3.1.9) |
4.3.2. Ejercicios
Determina si las siguientes cúbicas definen una curva elíptica en los cuerpos que se indican. Para aquellos casos en los que sea curva elíptica, halla todos los puntos de la curva. Recuerda que debes tener en cuenta el punto del infinito θE. Comprueba los resultados con la función ListarPuntos de la librería CurvasElipt.
a) ![]() con =
con = ![]() y
y ![]()
b) ![]() con con en
con con en ![]() y
y ![]()
c) ![]() con en
con en ![]() y
y ![]()
| > |
| > |
| > |
5. Aritmética de Curvas Elípticas
5.1. Introducción
Vamos a definir una suma sobre los puntos de una curva elíptica que nos permitirá, posteriormente, construir el criptosistema de curvas elípticas. En los siguientes apartados definiremos las operaciones necesarias. Por motivos didácticos, empezaremos introduciendo la suma de puntos de modo geométrico, para curvas elípticas sobre ℝ y después daremos el algoritmo general.
5.2. Suma de dos puntos de una Curva Elíptica e interpretación geométrica sobre ℝ
Dada una curva elíptica E, sobre ℝ, y dos puntos P = (![]() ,
, ![]() ), Q = (
), Q = (![]() ,
, ![]() ) ∈ E, podemos obtener un tercer punto de la curva operando como sigue:
) ∈ E, podemos obtener un tercer punto de la curva operando como sigue:
Calculamos la recta que pasa por P y Q. Dicha recta corta a la cúbica en otro punto R = (![]() ,
, ![]() ). Se define P + Q := R = (
). Se define P + Q := R = (![]() ,
, ![]() ), el simétrico de R respecto del eje X.
), el simétrico de R respecto del eje X.
Nota: Si la cúbica f (x) = ![]() + ax + b no tiene raíces múltiples, se puede demostrar que toda recta corta a la cúbica en tres puntos, contados con multiplicidad. Por tanto, la suma está bien definida.
+ ax + b no tiene raíces múltiples, se puede demostrar que toda recta corta a la cúbica en tres puntos, contados con multiplicidad. Por tanto, la suma está bien definida.
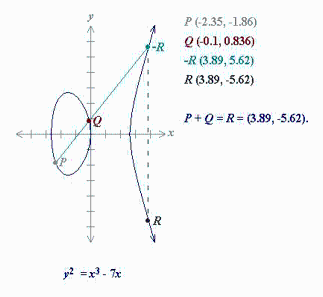
Representación gráfica de la suma de dos puntos P + Q = R.
Hay que tener en cuenta los siguientes casos especiales:
- Si P = Q, calculamos la recta tangente a la curva en P. Dicha recta corta a la cúbica en otro punto R = (![]() ,
, ![]() ). Se define 2 P = P + P := (
). Se define 2 P = P + P := (![]() ,
, ![]() ), el simétrico de R respecto del eje X.
), el simétrico de R respecto del eje X.
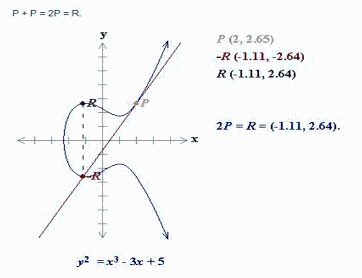
Representación gráfica de P + P = 2P.
- Si P = (![]() ,
, ![]() ) y Q = (
) y Q = (![]() ,
, ![]() ), es el simétrico de P respecto del eje X, la recta que une estos dos puntos tiene pendiente vertical. El tercer punto de corte con la cúbica es el punto del infinito, que podemos imaginarlo “al final” del eje Y. El simétrico de este punto vuelve a ser el propio punto del infinito. Por eso, se define P + (–P) := θE.
), es el simétrico de P respecto del eje X, la recta que une estos dos puntos tiene pendiente vertical. El tercer punto de corte con la cúbica es el punto del infinito, que podemos imaginarlo “al final” del eje Y. El simétrico de este punto vuelve a ser el propio punto del infinito. Por eso, se define P + (–P) := θE.
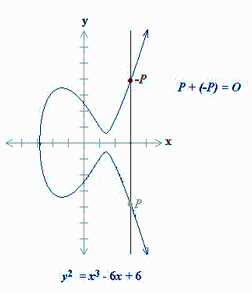
Representación gráfica de P + (–P) = θE.
- Si P = (![]() ,
, ![]() ) y Q = θE, el punto del infinito, la recta que une estos dos puntos tiene pendiente vertical. El tercer punto de corte con la cúbica es el simétrico de P respecto del eje X, el punto R = (
) y Q = θE, el punto del infinito, la recta que une estos dos puntos tiene pendiente vertical. El tercer punto de corte con la cúbica es el simétrico de P respecto del eje X, el punto R = (![]() ,
, ![]() ). El simétrico de R vuelve a ser el propio P. Por eso se define P +
). El simétrico de R vuelve a ser el propio P. Por eso se define P + ![]() := P.
:= P.
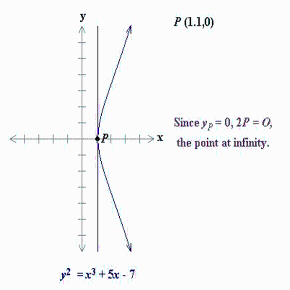
Representación gráfica de P + θE = P.
5.3. Algoritmo para la suma de dos puntos de una Curva Elíptica sobre
Sean E(): ![]() =
= ![]() + ax + b una curva elíptica y P1 = (x1, y1) y P2 = (x2, y2) puntos de la curva. Se define la suma P1 + P2 := (x3, y3) del siguiente modo:
+ ax + b una curva elíptica y P1 = (x1, y1) y P2 = (x2, y2) puntos de la curva. Se define la suma P1 + P2 := (x3, y3) del siguiente modo:
|
|
Además,
- Si m = ∞ entonces P1 + P2 := θE- Para todo P ∈ E: P + θE := P
Proposición
Se verifica que (E, +) es un grupo conmutativo, esto es:
(i) + es operación interna.(ii) + es asociativa.(iii) θE es elemento neutro para +.(iv) Todo elemento P ∈ E – {θE} tiene opuesto, que se denota – P. Además, si P = (x, y) entonces – P = (x, –y) y – θE = θE.(v) + es conmutativa.
5.3.1. Ejemplo
Vamos a calcular las sumas posibles entre los puntos de la curva ![]() en
en ![]() :
:
En primer lugar representamos los parámetros de la curva como variables:
| > | a:=1: b:=-2: n:=5: |
Ahora vamos a calcular todos los puntos de la curva, para ello tenemos que calcular los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to n-1 do cuadrados:={op(cuadrados),i&^2 mod n}; end do; |
| (5.3.1.1) |
Seguidamente calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados:
y comprobamos si son cuadrados:
| > | for i from 0 to n-1 do
raiz:=[i,(i^3+a*i+b) mod n]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (5.3.1.2) |
En vista de los resultados tenemos que f(1) y f(4) son cuadrados. Por tanto (1, ± ![]() ) = (1, ±0) y (4, ±
) = (1, ±0) y (4, ± ![]() ) = (4, ±1) son los únicos puntos de la curva en
) = (4, ±1) son los únicos puntos de la curva en ![]() ×
×![]() . Entonces
. Entonces ![]() en
en ![]() tiene 4 puntos: E(
tiene 4 puntos: E(![]() ) = {(1, 0), (4, 1), (4, 4), θE}
) = {(1, 0), (4, 1), (4, 4), θE}
A continuación, por medio de la función ListarPuntos comprobamos los resultados obteniendo la lista de los puntos de la curva y su representación gráfica:
| > | ListarPuntos(a,b,n,true); |
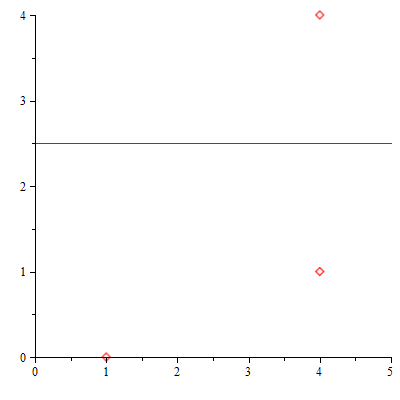 |
|
| (5.3.1.3) |
Ahora sumamos dos de los puntos utilizando las fórmulas, pero antes asignaremos los puntos a variables:
| > | P:=[1,0]: Q:=[4,1]: |
| > | mP_Q:=(Q[2]-P[2])/(Q[1]-P[1]) mod n;
x:=mP_Q^2-P[1]-Q[1] mod n; y:=mP_Q*(P[1]-x)-P[2] mod n; P_Q:=[x,y] mod n; |
| (5.3.1.4) |
Comprobamos el resultado con la función SumaPuntos y mostramos su representación gráfica:
| > | SumaPuntos(a,b,n,P,Q,true); |
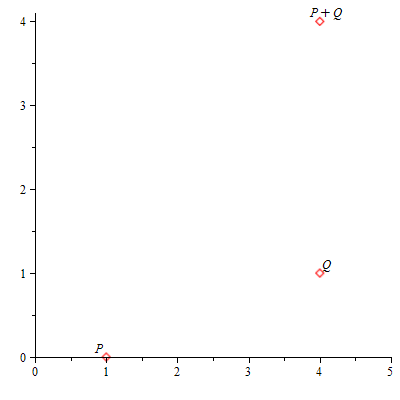 |
|
| (5.3.1.5) |
Ahora vamos a calcular el doble de uno de los puntos sumándolo consigo mismo:
| > | R:=[4,4]: |
| > | mR_R:=((3*(R[1]^2)+a)/(2*R[2])) mod n;
x:=mR_R^2-R[1]-R[1] mod n; y:=mR_R*(R[1]-x)-R[2] mod n; R_R:=[x,y] mod n; |
| (5.3.1.6) |
Comprobamos el resultado con la función SumaPuntos y mostramos su representación gráfica:
| > | SumaPuntos(a,b,n,R,R,true); |
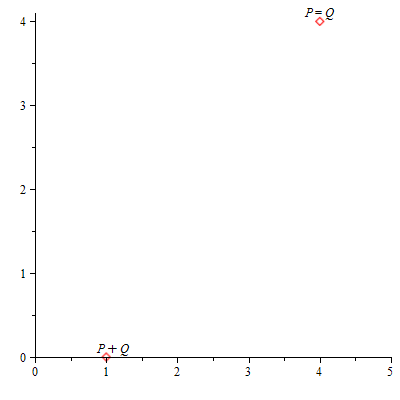 |
|
| (5.3.1.7) |
Seguidamente sumaremos los puntos P = (1,0) y R = (4,4):
| > | mP_R:=(R[2]-P[2])/(R[1]-P[1]) mod n;
x:=mP_R^2-P[1]-R[1] mod n; y:=mP_R*(P[1]-x)-P[2] mod n; P_R:=[x,y] mod n; |
| (5.3.1.8) |
Comprobamos que el resultado es correcto por medio de la función SumaPuntos :
| > | SumaPuntos(a,b,n,P,R); |
| (5.3.1.9) |
La siguiente suma que realizaremos es la de los puntos Q = (4,1) y R = (4,4):
| > | mQ_R:=(R[2]-Q[2])/(R[1]-Q[1]) mod n;
x:=mQ_R^2-Q[1]-R[1] mod n; y:=mQ_R*(Q[1]-x)-Q[2] mod n; Q_R:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (5.3.1.10) |
En este caso, al calcular mQ_R se produce una división por 0, por lo que Q+R = θE como podemos comprobar con la función SumaPuntos :
| > | SumaPuntos(a,b,n,Q,R,true); |
| (5.3.1.11) |
A continuación calcularemos P+P:
| > | mP_P:=((3*(P[1]^2)+a)/(2*P[2])) mod n;
x:=mP_P^2-P[1]-P[1] mod n; y:=mP_P*(P[1]-x)-P[2] mod n; P_P:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (5.3.1.12) |
En este caso, al calcular mP_P se produce una división por 0, por lo que P+P = θE como podemos comprobar con la función SumaPuntos :
| > | SumaPuntos(a,b,n,P,P,true); |
| (5.3.1.13) |
Finalmente procedemos a calcular la suma de Q+Q:
| > | mQ_Q:=((3*(Q[1]^2)+a)/(2*Q[2])) mod n;
x:=mQ_Q^2-Q[1]-Q[1] mod n; y:=mQ_Q*(Q[1]-x)-Q[2] mod n; Q_Q:=[x,y] mod n; |
| (5.3.1.14) |
Y comprobamos el resultado con la función SumaPuntos :
| > | SumaPuntos(a,b,n,Q,Q,true); |
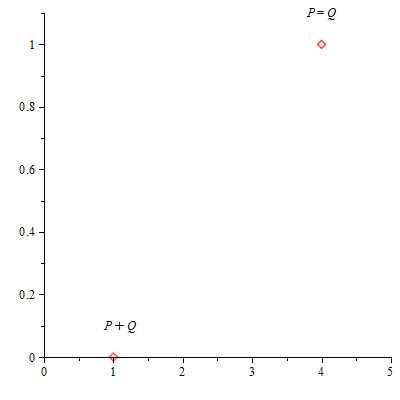 |
|
| (5.3.1.15) |
Por último, podemos comprobar que las sumas con correctas usando la función TablaSumas de la librería CurvasElipt:
| > | TablaSumas(a,b,n); |
 |
(5.3.1.16) |
Se han omitido los casos de suma con el punto del infinito puesto que para todo P ∈ E: P + θE := P.
5.3.2. Ejercicios
Calcula las sumas entre todos los puntos de la curva ![]()
![]() así como las sumas entre cualquier pareja de puntos. Comprueba los resultados con la función TablaSumas de la librería CurvasElipt:
así como las sumas entre cualquier pareja de puntos. Comprueba los resultados con la función TablaSumas de la librería CurvasElipt:
| > |
| > |
| > |
Dados el entero k ∈ ℤ y el punto P ∈ E, denotamos
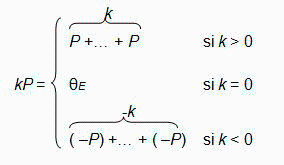 Dado P ∈ E() una curva elíptica, se llama conjunto de los múltiplos de P, y se denota < P >, al conjunto:
Dado P ∈ E() una curva elíptica, se llama conjunto de los múltiplos de P, y se denota < P >, al conjunto:
< P > = {k P / k ∈ ℤ}
5.4.1. Ejemplo
Vamos a calcular los múltiplos de uno del punto P = (4,1) de la curva ![]() en
en ![]() :
:
En primer lugar representamos los parámetros de la curva como variables:
| > | a:=1: b:=-2: n:=5: P:=[4,1]: |
A continuación, calculamos 2P = P+P:
| > | mP_2P:=((3*(P[1]^2)+a)/(2*P[2])) mod n;
x:=mP_2P^2-P[1]-P[1] mod n; y:=mP_2P*(P[1]-x)-P[2] mod n; P_2P:=[x,y] mod n; |
| (5.4.1.1) |
Lo comprobamos con la función SumaPuntos y con la función MúltiploPunto de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,P); |
| (5.4.1.2) |
| > | MúltiploPunto(a,b,n,2,P); |
| (5.4.1.3) |
Vemos que ambos resultados coinciden. Ahora vamos a calcular 3P = 2P + P:
| > | mP_3P:=(P_2P[2]-P[2])/(P_2P[1]-P[1]) mod n;
x:=mP_3P^2-P[1]-P_2P[1] mod n; y:=mP_3P*(P[1]-x)-P[2] mod n; P_3P:=[x,y] mod n; |
| (5.4.1.4) |
Lo comprobamos con la función SumaPuntos y con la función MúltiploPunto de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,P_2P); |
| (5.4.1.5) |
| > | MúltiploPunto(a,b,n,3,P); |
| (5.4.1.6) |
Vemos que ambos resultados coinciden. Ahora vamos a calcular 4P = 3P + P:
| > | mP_4P:=(P_3P[2]-P[2])/(P_3P[1]-P[1]) mod n;
x:=mP_4P^2-P[1]-P_3P[1] mod n; y:=mP_4P*(P[1]-x)-P[2] mod n; P_4P:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (5.4.1.7) |
En este caso, al calcular mP_4P se produce una división por 0, por lo que 3P+P = θE
Lo comprobamos con la función SumaPuntos y con la función MúltiploPunto de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,P_PP); |
| (5.4.1.8) |
| > | MúltiploPunto(a,b,n,4,P); |
| (5.4.1.9) |
Vemos de nuevo, que los resultados coinciden. Por último, vamos a calcular 5P = 4P + P:
Debido a que para todo P ∈ E: P + θE := P y 4P = θE, entonces 5P = P = (4,1)
Lo comprobamos con la función SumaPuntos y con la función MúltiploPunto de la librería CurvasElipt:
| > | P_PPP:=infinity: |
| > | SumaPuntos(a,b,n,P,P_PPP); |
| (5.4.1.10) |
| > | MúltiploPunto(a,b,n,5,P); |
| (5.4.1.11) |
Vemos que los resultados coinciden y que en ambos casos se obtiene (4,1). Si calculásemos 6P = 5P+P estaríamos en el mismo caso que P+P debido a que 5P = P = [4,1].
Dado P ∈ E() una curva elíptica, de modo análogo a como se define el orden de un número entero en un cuerpo finito, se puede definir el orden de un punto P de una curva elíptica, y lo denotamos ord(P) al menor entero positivo n, en caso de que exista, que verifica
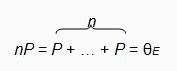
Si tal n no existe, diremos que P tiene orden infinito.
Si = ℤp, todos los puntos de E tienen orden finito ya que el conjunto de todos los múltiplos de P es un subconjunto de E, y se tiene que:
{rP / r ∈ ℤ} ⊆ E(ℤp) ⊆ ℤp × ℤp conjunto finito
Además card(< P >) = ord(P).
Vamos a calcular el orden del punto P = (1,2) de la curva elíptica ![]()
![]() . En primer lugar, asignamos los parámetros de la curva a variables:
. En primer lugar, asignamos los parámetros de la curva a variables:
| > | a:=0: b:=-2: n:=5: P:=[1,2]: |
A continuación, calculamos los múltiplos del punto P = (1,2) hasta encontrar el número k que cumpla ![]() .
.
En primer lugar calculamos 2P = P+P:
| > | mP_2P:=((3*(P[1]^2)+a)/(2*P[2])) mod n;
x:=mP_2P^2-P[1]-P[1] mod n; y:=mP_2P*(P[1]-x)-P[2] mod n; P_2P:=[x,y] mod n; |
| (5.5.1.1) |
Vemos que 2P = (2,1). Por no ser ![]() calculamos 3P = 2P+P:
calculamos 3P = 2P+P:
| > | mP_3P:=(P_P[2]-P[2])/(P_P[1]-P[1]) mod n;
x:=mP_3P^2-P[1]-P_P[1] mod n; y:=mP_3P*(P[1]-x)-P[2] mod n; P_3P:=[x,y] mod n; |
| (5.5.1.2) |
Vemos que 3P = (3,0). Por no ser ![]() calculamos 4P = 3P+P:
calculamos 4P = 3P+P:
| > | mP_4P:=(P_3P[2]-P[2])/(P_3P[1]-P[1]) mod n;
x:=mP_4P^2-P[1]-P_3P[1] mod n; y:=mP_4P*(P[1]-x)-P[2] mod n; P_4P:=[x,y] mod n; |
| (5.5.1.3) |
Vemos que 4P = (2,4). Por no ser ![]() calculamos 5P = 4P+P:
calculamos 5P = 4P+P:
| > | mP_5P:=(P_4P[2]-P[2])/(P_4P[1]-P[1]) mod n;
x:=mP_5P^2-P[1]-P_4P[1] mod n; y:=mP_5P*(P[1]-x)-P[2] mod n; P_5P:=[x,y] mod n; |
| (5.5.1.4) |
Vemos que 5P = (1,3). Por no ser ![]() calculamos 6P = 5P+P:
calculamos 6P = 5P+P:
| > | mP_6P:=(P_5P[2]-P[2])/(P_5P[1]-P[1]) mod n;
x:=mP_6P^2-P[1]-P_5P[1] mod n; y:=mP_6P*(P[1]-x)-P[2] mod n; P_6P:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (5.5.1.5) |
En este caso, al calcular mP_6P se produce una división por 0, por lo que 6P = 5P+P = θE y el orden del punto P = (1,2) es 6.
Por último, comprobamos que los cálculos anteriores son correctos con la función MúltiploPunto de la librería CurvasElipt:
| > | i:=1:
while MúltiploPunto(a,b,n,i,P) <> infinity do i:=i+1; od: i; |
| (5.5.1.6) |
Por lo tanto, se confirma que el orden del punto P = (1,2) de la curva elíptica ![]()
![]() es 6.
es 6.
5.5.2. Ejercicios
Calcula los órdenes de los puntos P = (6,4) y Q = (1,7) de la curva elíptica ![]()
![]() .
.
| > |
| > |
| > |
Obtener el número de puntos de una curva elíptica es un problema difícil.
Este teorema proporciona cotas para el cardinal de E(ℤp).
Teorema: Sea N el número de puntos de una curva elíptica E(ℤp): ![]() =
= ![]() + ax + b. Entonces
+ ax + b. Entonces
|N – (p + 1)| ≤ 2 ![]()
O, equivalentemente
(p + 1) – 2 ![]() ≤ N ≤ (p + 1) + 2
≤ N ≤ (p + 1) + 2 ![]()
En las condiciones anteriores, N ∈ O (p).
5.6.1. Ejemplo
¿Cuántos puntos puede tener una curva elíptiva de ![]() ? Utilizando las cotas del teorema anterior,
? Utilizando las cotas del teorema anterior,
| > | p:=5:
evalf((p+1)-2*p^(1/2)) <= N; N <= evalf((p+1)+2*p^(1/2)); |
| (5.6.1.1) |
Por tanto, el número de puntos de una curva elíptica en ![]() está en el rango 2..10.
está en el rango 2..10.
5.6.2. Ejercicios
Determina las cotas inferior y superior para el número de puntos de una curva elíptica cuando:
(a) = ![]()
(b) = ![]()
(c) = ![]()
| > |
| > |
| > |
Pueden existir curvas elípticas sobre ![]() con 31 puntos? ¿Y con 4?
con 31 puntos? ¿Y con 4?
| > |
| > |
| > |
5.7. Algoritmo eficiente para calcular múltiplos de un punto
Para la operación de cifrado interesa disponer de un algoritmo eficiente capaz de calcular los múltiplos de un punto. Se plantea el siguiente
PROBLEMA: Calcular kP con k ∈ ℤ, P ∈ E()
![]()
Hay varias formas de resolver el problema para esta instancia (y en el caso general):
a) Por la fuerza bruta: Se realizan 10 sumas, donde un sumando sería P y el otro la suma acumulada.
b) Método eficiente (calculando dobles): Si escribimos 11 en base 2 tenemos que 11 = (1011)2. Por tanto:
(1011)2P = (![]() +2 + 1)P = 2(2(2P)) + (2P) + P
+2 + 1)P = 2(2(2P)) + (2P) + P
Esto es, si almacenamos los múltiplos de P que son potencias de 2, el cálculo anterior requiere 5 sumas.
El siguiente algoritmo calcula kP de manera eficiente. Este algoritmo es análogo al de exponenciación rápida.
Dados P ∈ E(), k ∈ ℕ, para calcular kP se hace lo siguiente:
1. Si P = θE o bien k = 0 devolver θE. En otro caso definir s := θE (valor de la suma) c := P (múltiplos de P con escalar potencia de 2)
2. Definir q .= cociente de la división euclídea de k entre 2, r := resto de la división euclídea de k entre 2, Si r = 1 entonces s := c
3. Mientras q ≠ 0 hacer: c := 2c, q := cociente de la división euclídea de q entre 2, r := resto de la división euclídea de q entre 2, Si r = 1 entonces s := s + c.
4. Devolver s.
5.7.1. Ejemplo
Como pudimos ver en el ejemplo 5.5.1. para calcular el orden del punto P = (1,2) de la curva elíptica ![]()
![]() tuvimos que realizar 6 sumas. Según el algoritmo eficiente para calcular múltiplos de un punto tenemos que: 6P =
tuvimos que realizar 6 sumas. Según el algoritmo eficiente para calcular múltiplos de un punto tenemos que: 6P = ![]() P = (
P = (![]() )P = 2(2P) + 2P. De modo que, almacenando los múltiplos de P que son potencia de 2, sólo serían necesarias 3 sumas. Vamos a comprobarlo calculando 6P con el algoritmo eficiente:
)P = 2(2P) + 2P. De modo que, almacenando los múltiplos de P que son potencia de 2, sólo serían necesarias 3 sumas. Vamos a comprobarlo calculando 6P con el algoritmo eficiente:
En primer lugar asignamos los parámetros de la curva a variables:
| > | a:=0: b:=-2: n:=5: P:=[1,2]: k:=6: |
1. Vemos que P no es θE ni k es 0, por lo que definimos s (el valor de la suma) y c (los múltiplos de P con escalar potencia de 2):
| > | s:=infinity; c:=P; |
| (5.7.1.1) |
2. Definimos q (cociente de la división euclídea de k entre 2) y r (resto de la división euclídea de k entre 2):
| > | q:=iquo(abs(k),2,'r');
r; |
| (5.7.1.2) |
Como r = 0, no realizamos la asignación s := c.
3. Como q es distinto de 0, tenemos que seguir haciendo los siguientes cálculos:
| > | c:=SumaPuntos(a,b,n,c,c);
q:=iquo(abs(q),2,'r'); r; |
| (5.7.1.3) |
Tenemos que r = 1, por lo que realizamos la asignación s := s + c.
| > | s:=SumaPuntos(a,b,n,s,c); |
| (5.7.1.4) |
Como q es distinto de 0, seguimos realizantdo los cálculos:
| > | c:=SumaPuntos(a,b,n,c,c);
q:=iquo(abs(q),2,'r'); r; |
| (5.7.1.5) |
Tenemos que r = 1, por lo que realizamos la asignación s := s + c.
| > | s:=SumaPuntos(a,b,n,s,c); |
| (5.7.1.6) |
Como q = 0, devolvemos s, ya que contiene 6P:
| > | s; |
| (5.7.1.7) |
Comprobamos el resultado mediante la función MúltiploPunto de la librería CurvasElipt y que utiliza el algoritmo eficiente para calcular múltiplos de un punto:
| > | MúltiploPunto(a,b,n,k,P); |
| (5.7.1.8) |
Vemos que los resultados coinciden. Para ver de una manera más clara el funcionamiento del algoritmo, lo podemos resumir en una tabla (i = nº de iteración; q = cociente de la división euclídea; r = resto de la división euclídea; s = valor de la suma; c = múltiplos de P con escalar potencia de 2):
i |
q |
r |
s |
c |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
5.7.2. Ejercicios
Aplica el algoritmo anterior para calcular 11P, siendo P = (1,5) un punto de la curva eliptica E(![]() ):
): ![]() que puedes encontrar en el capítulo Recursos como #Curva17. Comprueba el resultado mediante la función MúltiploPunto de la librería CurvasElipt.
que puedes encontrar en el capítulo Recursos como #Curva17. Comprueba el resultado mediante la función MúltiploPunto de la librería CurvasElipt.
| > |
| > |
| > |
5.8. Problema del logaritmo discreto sobre Curvas Elípticas
Como hemos dicho, el criptosistema ElGamal basa su seguridad en la dificultad del problema del logaritmo discreto. Del mismo modo, la seguridad del criptosistema de curvas elípticas se basa en un problema intratable de la teoría de números. Calcular los múltiplos de un punto P, ({P, 2P, 3P, …}), es un problema sencillo pues se pueden obtener de manera eficiente, pero dado Q un punto de la curva, averiguar k ∈ ℤ, tal que Q = kP es un problema computacionalmente costoso, que por analogía se denomina problema de Logaritmo Discreto sobre curvas elípticas.Si E(ℤp) es una curva elíptica y B es un punto de E, el problema del logaritmo discreto de base B consiste en:
Dado P ∈ E, calcular el entero k, caso de que exista, de manera que kB = P.
Los algoritmos conocidos para calcular logaritmos discretos sobre curvas elípticas son de complejidad exponencial.
5.8.1. Ejemplo
Vamos a calcular varios múltiplos del punto P = (565,194) de la curva elíptica E(![]() ):
): ![]() para hallar a partir de P y su múltiplo, el entero por el que ha sido multiplicado para calcularlo.
para hallar a partir de P y su múltiplo, el entero por el que ha sido multiplicado para calcularlo.
En primer lugar asignamos los parámetros de la curva a variables:
| > | a:=-1: b:=188: n:=751: P:=[565, 194]: |
A continuación calculamos los múltiplos 10, 100 y 750 del punto P:
| > | P_10:=MúltiploPunto(a,b,n,10,P); |
| (5.8.1.1) |
| > | P_100:=MúltiploPunto(a,b,n,100,P); |
| (5.8.1.2) |
| > | P_750:=MúltiploPunto(a,b,n,750,P); |
| (5.8.1.3) |
A continuación utilizaremos la función time para calcular el tiempo que tarda la función LogaritmoPunto de la librería CurvasElipt en calcular k, caso de que exista, de manera que kB = P:
| > | t:=time(); |
| (5.8.1.4) |
| > | LD_10=LogaritmoPunto(a,b,n,P,P_10); |
| (5.8.1.5) |
| > | t_10:=time()-t; |
| (5.8.1.6) |
| > | t:=time(); |
| (5.8.1.7) |
| > | LD_100=LogaritmoPunto(a,b,n,P,P_100); |
| (5.8.1.8) |
| > | t_100:=time()-t; |
| (5.8.1.9) |
| > | t:=time(); |
| (5.8.1.10) |
| > | LD_750=LogaritmoPunto(a,b,n,P,P_750); |
| (5.8.1.11) |
| > | t_750:=time()-t; |
| (5.8.1.12) |
Para k = 10 y k = 100 hemos recuperado justamente el mismo valor de k introducido al obtener el múltiplo. En cambio para k = 750 el orden del punto es menor que dicho valor y la función LogaritmoPunto ha encontrado un valor para k más pequeño que cumple (575,329) = k (565,194).
5.8.2. Ejercicios
Dados los puntos B = (29876406597393, 252423417455518) y P = (![]() ) de la curva
) de la curva ![]() en
en ![]() que puedes encontrar en el capítulo Recursos como #Curva16, calcula el valor de k tal que kB = P. Comprueba el resultado mediante la función LogaritmoPunto de la librería CurvasElipt.
que puedes encontrar en el capítulo Recursos como #Curva16, calcula el valor de k tal que kB = P. Comprueba el resultado mediante la función LogaritmoPunto de la librería CurvasElipt.
| > |
| > |
| > |
6. Criptosistema de Curvas Elípticas
6.1. Representación de texto como punto de una curva
En los sistemas criptográficos debemos disponer de algún método que transforme el mensaje en un equivalente numérico con el que realizar las operaciones de encriptado. Puesto que en este caso vamos a utilizar las curvas como objeto para cifrar, necesitamos una estrategia que permita representar el texto en claro m (o su equivalente numérico) como un punto de la curva elíptica Pm = (xm , ym ) que guarde relación con el mensaje. Al respecto hay que decir que:
Dada una curva elíptica arbitraria E(ℤp) no existe un algoritmo determinista y polinómico en log(p) que liste un número suficientemente grande de puntos de la curva.Existen algoritmos probabilísticos que buscan puntos de una curva con una probabilidad de fallo tan baja como se quiera.
El procedimiento que se describe a continuación se debe a Koblitz.![]() La estrategia se basa en el hecho de que aproximadamente la mitad de los valores de ℤp son cuadrados. Por tanto, la probabilidad de que un elemento de ℤp elegido al azar no sea un cuadrado es aproximadamente 1/2. De donde, dada la curva E(ℤp):
La estrategia se basa en el hecho de que aproximadamente la mitad de los valores de ℤp son cuadrados. Por tanto, la probabilidad de que un elemento de ℤp elegido al azar no sea un cuadrado es aproximadamente 1/2. De donde, dada la curva E(ℤp): ![]() =
= ![]() + ax + b la probabilidad de que
+ ax + b la probabilidad de que ![]() + ax + b no sea un cuadrado es aproximadamente 1/2.
+ ax + b no sea un cuadrado es aproximadamente 1/2.
El siguiente algoritmo muestra el procedimiento de paso de un símbolo a un punto de la curva:
Dados la curva E(ℤp): ![]() =
= ![]() + ax + b y un símbolo m ∈ ℤp :
+ ax + b y un símbolo m ∈ ℤp :
Elegimos k suficientemente grande de modo que ![]() , la probabilidad de fallo al representar m como un punto de E sea aceptable y además mk < p. Sea j un valor en el rango 0..k – 1
, la probabilidad de fallo al representar m como un punto de E sea aceptable y además mk < p. Sea j un valor en el rango 0..k – 1
Asignamos j := 0
Mientras j < k, hacer
x := mk + j (con lo que x está comprendido entre mk y (mk + k -1))si ![]() + ax + b es un cuadrado de ℤp entonces devolver Pm := (x,
+ ax + b es un cuadrado de ℤp entonces devolver Pm := (x, ![]() ) (que es un punto de la curva) Si j = k fallo.
) (que es un punto de la curva) Si j = k fallo.
El proceso anterior se detiene cuando ![]() + ax + b es un cuadrado de ℤp o bien cuando j > k – 1. Puesto que la probabilidad de que
+ ax + b es un cuadrado de ℤp o bien cuando j > k – 1. Puesto que la probabilidad de que ![]() + ax + b no sea un cuadrado es aproximadamente 1/2, tras k iteraciones la probabilidad de fallo es de
+ ax + b no sea un cuadrado es aproximadamente 1/2, tras k iteraciones la probabilidad de fallo es de ![]()
El proceso inverso, el paso de punto a número, es bastante sencillo:
x = mk + j → ![]() = m +
= m + ![]() → ⌊
→ ⌊![]() ⌋ = ⌊m +
⌋ = ⌊m + ![]() ⌋ = m, pues
⌋ = m, pues ![]() < 1 ( ⌊
< 1 ( ⌊![]() ⌋ es la función parte entera de x)
⌋ es la función parte entera de x)
De este modo, para recuperar el número a partir de las coordenadas del punto
Pm := (x, y) basta con calcular ⌊![]() ⌋
⌋
Por ejemplo, consideramos la curva E(ℤ4177): ![]() =
= ![]() + 3x. Se quieren representar dos símbolos, dados por sus equivalentes numéricos, m1 := 21 y m2 := 120, como puntos de la curva, con la mayor probabilidad de éxito. Como el mayor de estos números es m2, debe verificarse que:
+ 3x. Se quieren representar dos símbolos, dados por sus equivalentes numéricos, m1 := 21 y m2 := 120, como puntos de la curva, con la mayor probabilidad de éxito. Como el mayor de estos números es m2, debe verificarse que:
k • 120 < 4177→ k < ![]() = 34.808 → k ≤ 34
= 34.808 → k ≤ 34
Vamos a representar m1 := 21 como un punto de la curva siguiendo el procedimiento anterior y utilizando k := 34. Recordamos que x := mk + j.
Para j = 0, se tiene que x := 34 • 21 = 714. Evaluamos ![]() + 3 • 714 = 175, que no es un cuadrado en ℤ4177.
+ 3 • 714 = 175, que no es un cuadrado en ℤ4177.
Para j = 1, se tiene que x := 34 • 21 + 1 = 715. Evaluamos ![]() + 3 • 715 = 2927, que sí es un cuadrado en ℤ4177 y una raíz es 1161. Por tanto, el mensaje
+ 3 • 715 = 2927, que sí es un cuadrado en ℤ4177 y una raíz es 1161. Por tanto, el mensaje ![]() := 21 se representa mediante el punto de la curva (715, 1161).
:= 21 se representa mediante el punto de la curva (715, 1161).
Vamos a recuperar el mensaje a partir del punto:⌊![]() ⌋ = ⌊21.029⌋ = 21
⌋ = ⌊21.029⌋ = 21
6.1.1. Ejemplo
Vamos a utilizar las funciones TextoPunto y PuntoTexto de la librería CurvasElipt para representar la palabra OCA como puntos de la curva ![]() en
en ![]()
| > | a:=-2: b:=50: n:=1000000000000037: |
Aplicamos la función TextoPunto sobre el símbolo para representarlo como punto de la curva elíptica y la función PuntoTexto para recuperarlo:
| > | Primera:=TextoPunto(a,b,n,"O",castellano,12345); |
| (6.1.1.1) |
| > | PuntoTexto(a,b,n,Primera,castellano,12345); |
| (6.1.1.2) |
| > | Segunda:=TextoPunto(a,b,n,"C",castellano,12345); |
| (6.1.1.3) |
| > | PuntoTexto(a,b,n,Segunda,castellano,12345); |
| (6.1.1.4) |
| > | Tercera:=TextoPunto(a,b,n,"A",castellano,12345); |
| (6.1.1.5) |
| > | PuntoTexto(a,b,n,Tercera,castellano,12345); |
| (6.1.1.6) |
Nota: El valor 12345 de las funciones TextoPunto y PuntoTexto se corresponde con el parámetro k y es válido para cualquier letra del castellano si n=10000000000037. Para elegir k lo único que hace falta es que se cumpla m · k < n, donde m es la longitud del alfabeto. En el caso de utilizarse el alfabeto castellano de la librería CurvasElipt se tiene que cumplir que 113 · k < n.
6.1.2. Ejercicios
Utiliza las funciones TextoPunto y PuntoTexto de la librería CurvasElipt para representar los símbolos del alfabeto [A, B, C, D, E, F]. Para ello utiliza la curva ![]() en
en ![]() que puedes encontrar en el capítulo Recursos como #Curva16:
que puedes encontrar en el capítulo Recursos como #Curva16:
| > |
| > |
| > |
Las claves privada y pública en el criptosistema de curvas elípticas, se obtienen como sigue:
1. Comenzamos con un cuerpo ℤp conocido, con p ≠ 2,3, una curva elíptica E(ℤp), y un punto base B de dicha curva. (No necesitamos conocer el número de puntos de la curva).
2. Cada usuario j elige un entero de manera aleatoria, pongamos aj, que guarda en secreto, calcula el punto aj B y lo publica. La clave privada será aj y la clave pública será aj B.
La seguridad de estas claves se basa en la complejidad exponencial del problema del logaritmo discreto sobre curvas elípticas que debería resolver un espía para poder obtener aj a partir de aj B.
6.2.1. Ejemplo
Vamos a generar una clave de 3 dígitos utilizando la función GeneraClaveCE de la librería CurvasElipt. Para ello hay que introducir como parámetros una curva elíptica, un punto base de ésta, el tamaño de clave (que será el número de dígitos que queramos que tenga aj ) y un nombre para almacenar la clave privada. Utilizaremos la curva ![]() en
en ![]() con el punto base [565, 194].
con el punto base [565, 194].
Para ello asignamos los parámetros de la curva elíptica a variables y llamamos a la función GeneraClaveCE:
| > | a:=-1: b:=188: n:=751: base:=[565, 194]: |
| > | pública:=GeneraClaveCE(a,b,n,base,3,privada); |
| (6.2.1.1) |
| > | privada; |
| (6.2.1.2) |
A continuación vamos a comprobar que se ha generado correctamente:
| > | MúltiploPunto(a,b,n,privada[1],pública[2]); |
| (6.2.1.3) |
Comprobamos que el resultado coincide:
| > | is(% = pública[1]); |
| (6.2.1.4) |
6.2.2. Ejercicios
Utiliza la función GeneraClaveCE de la librería CurvasElipt para crear claves de 5, 10 y 15 dígitos. Para ello utiliza la curva ![]() en
en ![]() con el punto base [29876406597393, 252423417455518] que puedes encontrar en el capítulo Recursos como #Curva16:
con el punto base [29876406597393, 252423417455518] que puedes encontrar en el capítulo Recursos como #Curva16:
| > |
| > |
| > |
1. Para enviar el mensaje Pm al usuario i, cuya clave pública es ai B, el usuario j elige un entero arbitrario k y manda el par de puntos (kB, Pm + k (ai B)).
2. Para recuperar el mensaje en claro, el usuario i multiplica el primer punto del par por su clave secreta ai y el resultado se lo resta al segundo punto del par:
Pm + k (ai B) – ai (kB) = Pm + k (ai B) – k (ai B) = Pm
Así, el usuario j envía el mensaje Pm camuflado junto con la “pista” kB que, en principio, es suficiente para desenmascarar el mensaje sólo en el caso de ser el receptor autorizado. Obsérvese que no es necesario publicar el valor de K elegido
6.3.1. Ejemplo
Vamos a generar una clave con la que poder cifrar y descifrar un mensaje. Utilizaremos la curva ![]() en
en ![]() con el punto base [14619, 6880].
con el punto base [14619, 6880].
En primer lugar asignamos los parámetros de la curva elíptica a variables:
| > | a:=-2: b:=50: n:=14831: base:=[14619, 6880]: |
Seguidamente generamos la clave:
| > | clavep:=GeneraClaveCE(a,b,n,base,3,priv); |
| (6.3.1.1) |
A continuación, utilizamos la función CifrarCE para cifrar el mensaje por medio de este criptosistema. A esta función tenemos que indicarle el mensaje, el alfabeto sobre el que vamos a cifrar y la clave pública:
| > | men:="PATATA"; |
| (6.3.1.2) |
| > | cript:=CifrarCE(a,b,n,men,castellano,clavep); |
| (6.3.1.3) |
Obsérvese que el cifrado de "A" es diferente en las tres ocasiones. Eso se debe a la variación de la elección de K en cada caso.
Por último, utilizamos la función DescifrarCE para descifrar el criptograma anterior. Para ello tendremos que indicarle el criptograma, el alfabeto sobre el que vamos a decodificar y la clave privada:
| > | DescifrarCE(a,b,n,cript,castellano,priv); |
| (6.3.1.4) |
6.3.2. Ejercicios
Supón dos usuarios, Alicia y Bob, que quieren enviarse mensajes de modo seguro. Sigue el esquema anteriormente explicado: crea un mensaje de texto y cífralo para que Bob se lo envíe a Alicia. Una vez que Bob lo haya recibido, desencríptalo para comprobar que el resultado es correcto. Se recomienda la utilización de las funciones para cifrar y descifrar CifrarCE y DescifrarCE de la librería CurvasElipt. Para ello utiliza la curva ![]() en
en ![]() con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15:
con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15:
| > |
| > |
| > |
6.4. Elección de punto y curva
Hay varios modos de elegir una curva elíptica y un punto base B. Una vez que elegimos el cuerpo finito ℤp, podemos fijar una curva E(ℤp) y un punto B = (x, y) ∈ E(ℤp) al mismo tiempo.
1. Tomamos x, y, a tres elementos cualesquiera de ℤp
2. Calculamos b := ![]() – (
– (![]() + ax)
+ ax)
3. Comprobamos que ![]() + ax + b no tiene raíces múltiples (esto es, que 4
+ ax + b no tiene raíces múltiples (esto es, que 4 ![]() + 27
+ 27![]() ≠ 0). Si esta condición no se verifica, volvemos al punto 1.
≠ 0). Si esta condición no se verifica, volvemos al punto 1.
4. Fijamos B := (x, y) el punto de la curva elíptica.
6.4.1. Ejemplo
Vamos a buscar una curva elíptica en ![]() . Para ello utilizaremos el algoritmo explicado anteriormente:
. Para ello utilizaremos el algoritmo explicado anteriormente:
1. Tomamos tres elementos cualesquiera de ℤp que llamaremos x, y, a.
| > | x:=3; y:=5; a:=1; |
| (6.4.1.1) |
2. Calculamos b := ![]() – (
– (![]() + ax)
+ ax)
| > | b:= y^2 -(x^3 + a*x) mod 7; |
| (6.4.1.2) |
3. Comprobamos que ![]() + ax + b no tiene raíces múltiples (esto es, que 4
+ ax + b no tiene raíces múltiples (esto es, que 4 ![]() + 27
+ 27![]() ≠ 0). Si esta condición no se verifica, volvemos al punto 1.
≠ 0). Si esta condición no se verifica, volvemos al punto 1.
| > | is(4*a^3 + 27*b^2 mod 7 <> 0); |
| (6.4.1.3) |
Como no se ha verificado la condición anterior, volvemos al punto1:
1. Tomamos tres elementos cualesquiera de ℤp que llamaremos x, y, a.
| > | x:=3; y:=5; a:=2; |
| (6.4.1.4) |
2. Calculamos b := ![]() – (
– (![]() + ax)
+ ax)
| > | b:= y^2 -(x^3 + a*x) mod 7; |
| (6.4.1.5) |
3. Comprobamos que ![]() + ax + b no tiene raíces múltiples (esto es, que 4
+ ax + b no tiene raíces múltiples (esto es, que 4 ![]() + 27
+ 27![]() ≠ 0). Si esta condición no se verifica, volvemos al punto 1.
≠ 0). Si esta condición no se verifica, volvemos al punto 1.
| > | is((4*a^3 + 27*b^2 mod 7 <> 0)); |
| (6.4.1.6) |
4. Fijamos B := (x, y) el punto de la curva elíptica.
| > | B:=[x,y]; |
| (6.4.1.7) |
Por último, fijamos a y b:
| > | a:=a mod 7; b:=b mod 7; |
| (6.4.1.8) |
Por lo tanto la curva será ![]() en
en ![]() y B = [3,5] un punto de la curva.
y B = [3,5] un punto de la curva.
6.4.2. Ejercicios
Calcula una curva elíptica que tenga, al menos, 13 puntos y determina un punto base para ésta.
| > |
| > |
| > |
7. Comparativa entre ElGamal y CurvasElípticas
7.1. Planteamiento
Dado que en el breve recorrido histórico del primer apartado de este curso comentamos que las claves generadas para el criptosistema de Curvas Elípticas proporcionan mayor seguridad para un tamaño de clave menor, proponemos una serie de ejercicios con el objetivo de mostrar, justificar y comprobar de primera mano esta circunstancia.
Para ello, generaremos claves de diferentes tamaños para ambos criptosistemas. Como tanto el criptosistema ElGamal como el de Curvas Elípticas basan su seguridad en el problema del logaritmo discreto, utilizaremos las funciones correspondientes de la líbrería CurvasElipt para tratar de romper las claves.
7.2. Ejemplo
Vamos a generar una clave de 5 dígitos para el criptosistema de ElGamal y otra para el criptosistema de Curvas Elípticas para comparar sus criptoanálisis. Utilizaremos la curva ![]() en
en ![]() con el punto base [565, 194].
con el punto base [565, 194].
| > | a:=-1: b:=188: n:=751: base:=[565, 194]: |
En primer lugar generamos una clave para el criptosistema de ElGamal:
| > | claveEG:=GeneraClaveGamal(5,privEG); |
| (7.2.1) |
| > | privEG; |
| (7.2.2) |
Aplicamos el criptoanálisis a esta clave por medio de la función LogatirmoDiscreto de la librería CurvasElipt:
| > | t:=time(); |
| (7.2.3) |
| > | criptoanálisisEG:=LogaritmoDiscreto(claveEG[2],claveEG[1],claveEG[3]); |
| (7.2.4) |
| > | tEG:=time()-t; |
| (7.2.5) |
| > | is(criptoanálisisEG = privEG[2]); |
| (7.2.6) |
A continuación generamos una clave para el criptosistema de Curvas Elípticas:
| > | claveCE:=GeneraClaveCE(a,b,n,base,5,privCE); |
| (7.2.7) |
| > | privCE; |
| (7.2.8) |
Aplicamos el criptoanálisis a esta clave por medio de la función LogaritmoPunto de la librería CurvasElipt:
| > | t:=time(); |
| (7.2.9) |
| > | criptoanálisisCE:=LogaritmoPunto(a,b,n,claveCE[2],claveCE[1]); |
| (7.2.10) |
| > | tCE:=time()-t; |
| (7.2.11) |
| > | is(criptoanálisisCE = privCE[1]); |
| (7.2.12) |
Comparamos los tiempos:
| > | is(tEG < tCE); |
| (7.2.13) |
Como vemos, el tiempo del criptoanálisis para Curvas Elípticas es mayor que el de ElGamal. Por ello, se puede comprobar empíricamente en este caso que para claves del mismo tamaño es más seguro el criptosistema de Curvas Elípticas.
7.3. Ejercicios
Genera claves de tamaño 1 a 6 dígitos para el criptosistema de ElGamal y para el criptosistema de Curvas Elípticas. A continuación, realiza el criptoanálisis de cada una de ellas y guarda sus tiempos de ejecución. Compara los resultados obtenidos. ¿Qué conclusiones obtienes?
Recomendación: utiliza la cúbica ![]() en
en ![]() con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15. Si lo deseas, puedes escoger otra cúbica de la colección de curvas elípticas del capítulo Recursos.
con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15. Si lo deseas, puedes escoger otra cúbica de la colección de curvas elípticas del capítulo Recursos.
| > |
| > |
| > |
Colección de textos y frases
Frases
Las siguientes frases se pueden utilizar como mensajes a la hora de realizar los ejercicios o, simplemente, como herramienta a utilizar en el desarrollo y el manejo de la librería CurvasElipt.
| > | frase1:="¡Poderoso caballero es don dinero! Francisco de Quevedo.":
frase2:="El veloz murciélago hindú comía feliz cardillo y kiwi. La cigüeña tocaba el saxofón detrás del palenque de paja. Pangrama": frase3:="Esto es un mensaje de prueba ¡A ver qué pasa!": frase4:="NO DEJES PARA MAÑANA LO QUE PUEDAS HACER HOY. REFRANERO.": frase5:="El 2 de mayo de 1808 comenzó la Guerra de la Independencia.": frase6:="EL BUENO SERÁ SIEMPRE LIBRE AUNQUE SEA ESCLAVO; EL MALO SERÁ SIEMPRE ESCLAVO AUNQUE SEA REY. Marco Valerio Marcial.": frase7:="Lo bueno, si breve, dos veces bueno. Baltasar Gracián.": frase8:="EL QUE APRENDE Y APRENDE Y NO PRACTICA LO QUE SABE, ES COMO EL QUE ARA Y ARA Y NO SIEMBRA. Platón.": frase9:="Yo envié a mis naves a luchar contra los hombres, no contra las tempestades. Doy gracias a Dios de que me haya dejado recursos para soportar tal pérdida: y no creo importe mucho que nos hayan cortado las ramas con tal de que quede el árbol de donde han salido y puedan salir otras. Felipe II": frase10:="\"It's okay to make mistakes in Science. In fact, that's how we discover a lot of new things.\" Carol Lewis": frase11:="LA INTELIGENCIA ES LA HABILIDAD DE ADAPTARSE A LOS CAMBIOS. Stephen William Hawking.": frase12:="LO MEJOR ES SALIR DE LA VIDA COMO DE UNA FIESTA, NI SEDIENTO NI BEBIDO. Aristóteles.": frase13:="SI SE SABE EXACTAMENTE LO QUE SE VA A HACER, ¿PARA QUÉ HACERLO? Pablo Ruíz Picasso.": frase14:="Los viejos desconfían de la juventud porque han sido jóvenes. Shakespeare.": frase15:="¡El mundo está desquiciado! ¡Vaya faena, haber nacido yo para tener que arreglarlo! W. Shakespeare, Hamlet.": fraseErr:="«HOLA»": # Prueba con símbolos erróneos |
Textos
Las siguientes frases se pueden utilizar como mensajes a la hora de realizar los ejercicios o, simplemente, como herramienta a utilizar en el desarrollo y el manejo de la librería CurvasElipt.
El texto 1 es el poema "Poderoso Caballero es Don Dinero" de Francisco de Quevedo. Tiene 1173 caracteres.
| > | texto1:="Madre, yo al oro me humillo, Él es mi amante y mi amado, Pues de puro enamorado Anda continuo amarillo. Que pues doblón o sencillo Hace todo cuanto quiero, Poderoso caballero Es don Dinero. Nace en las Indias honrado, Donde el mundo le acompaña; Viene a morir en España, Y es en Génova enterrado. Y pues quien le trae al lado Es hermoso, aunque sea fiero, Poderoso caballero Es don Dinero. Son sus padres principales, Y es de nobles descendiente, Porque en las venas de Oriente Todas las sangres son Reales.Y pues es quien hace iguales Al rico y al pordiosero, Poderoso caballero Es don Dinero. ¿A quién no le maravilla Ver en su gloria, sin tasa, Que es lo más ruin de su casa Doña Blanca de Castilla? Mas pues que su fuerza humilla Al cobarde y al guerrero, Poderoso caballero Es don Dinero. Es tanta su majestad, Aunque son sus duelos hartos, Que aun con estar hecho cuartos No pierde su calidad. Pero pues da autoridad Al gañán y al jornalero, Poderoso caballero Es don Dinero. Más valen en cualquier tierra (Mirad si es harto sagaz) Sus escudos en la paz Que rodelas en la guerra. Pues al natural destierra Y hace propio al forastero, Poderoso caballero Es don Dinero.": |
El texto 2 es "La Canción del Pirata" de José de Espronceda. Tiene 2160 caracteres.
| > | texto2:="Con diez cañones por banda, viento en popa, a toda vela, no corta el mar, sino vuela un velero bergantín. Bajel pirata que llaman, por su bravura, El Temido, en todo mar conocido del uno al otro confín. La luna en el mar riela en la lona gime el viento, y alza en blando movimiento olas de plata y azul; y va el capitán pirata, cantando alegre en la popa, Asia a un lado, al otro Europa, y allá a su frente Istambul: Navega, velero mío sin temor, que ni enemigo navío ni tormenta, ni bonanza tu rumbo a torcer alcanza, ni a sujetar tu valor. Veinte presas hemos hecho a despecho del inglés y han rendido sus pendones cien naciones a mis pies. Que es mi barco mi tesoro, que es mi dios la libertad, mi ley, la fuerza y el viento, mi única patria, la mar. Allá; muevan feroz guerra ciegos reyes por un palmo más de tierra; que yo aquí; tengo por mío cuanto abarca el mar bravío, a quien nadie impuso leyes. Y no hay playa, sea cualquiera, ni bandera de esplendor, que no sienta mi derecho y dé pechos mi valor. Que es mi barco mi tesoro, que es mi dios la libertad, mi ley, la fuerza y el viento, mi única patria, la mar. A la voz de \"¡barco viene!\" es de ver cómo vira y se previene a todo trapo a escapar; que yo soy el rey del mar, y mi furia es de temer. En las presas yo divido lo cogido por igual; sólo quiero por riqueza la belleza sin rival. Que es mi barco mi tesoro, que es mi dios la libertad, mi ley, la fuerza y el viento, mi única patria, la mar. ¡Sentenciado estoy a muerte! Yo me río no me abandone la suerte, y al mismo que me condena, colgaré de alguna antena, quizá; en su propio navío Y si caigo, ¿qué es la vida? Por perdida ya la di, cuando el yugo del esclavo, como un bravo, sacudí. Que es mi barco mi tesoro, que es mi dios la libertad, mi ley, la fuerza y el viento, mi única patria, la mar. Son mi música mejor aquilones, el estrépito y temblor de los cables sacudidos, del negro mar los bramidos y el rugir de mis cañones. Y del trueno al son violento, y del viento al rebramar, yo me duermo sosegado, arrullado por el mar. Que es mi barco mi tesoro, que es mi dios la libertad, mi ley, la fuerza y el viento, mi única patria, la mar.": |
El texto 3 es un fragmento del capítulo I de "El Ingenioso Hidalgo Don Quijote de la Mancha" de Miguel de Cervantes. Tiene 5048 caracteres.
| > | texto3:="En un lugar de la Mancha, de cuyo nombre no quiero acordarme, no ha mucho tiempo que vivía un hidalgo de los de lanza en astillero, adarga antigua, rocín flaco y galgo corredor. Una olla de algo más vaca que carnero, salpicón las más noches, duelos y quebrantos los sábados, lantejas los viernes, algún palomino de añadidura los domingos, consumían las tres partes de su hacienda. El resto della concluían sayo de velarte, calzas de velludo para las fiestas, con sus pantuflos de lo mesmo, y los días de entresemana se honraba con su vellorí de lo más fino. Tenía en su casa una ama que pasaba de los cuarenta, y una sobrina que no llegaba a los veinte, y un mozo de campo y plaza, que así ensillaba el rocín como tomaba la podadera. Frisaba la edad de nuestro hidalgo con los cincuenta años; era de complexión recia, seco de carnes, enjuto de rostro, gran madrugador y amigo de la caza. Quieren decir que tenía el sobrenombre de Quijada, o Quesada, que en esto hay alguna diferencia en los autores que deste casoescriben; aunque, por conjeturas verosímiles, se deja entender que se llamaba Quejana. Pero esto importa poco a nuestro cuento; basta que en la narración dél no se salga un punto de la verdad. Es, pues, de saber que este sobredicho hidalgo, los ratos que estaba ocioso, que eran los más del año, se daba a leer libros de caballerías, con tanta afición y gusto, que olvidó casi de todo punto el ejercicio de la caza, y aun la administración de su hacienda. Y llegó a tanto su curiosidad y desatino en esto, que vendió muchas hanegas de tierra de sembradura para comprar libros de caballerías en que leer, y así, llevó a su casa todos cuantos pudo haber dellos; y de todos, ningunos le parecían tan bien como los que compuso el famoso Feliciano de Silva, porque la claridad de su prosa y aquellas entricadas razones suyas le parecían de perlas, y más cuando llegaba a leer aquellos requiebros y cartas de desafíos, donde en muchas partes hallaba escrito: La razón de la sinrazón que a mi razón se hace, de tal manera mi razón enflaquece, que con razón me quejo de la vuestra fermosura. Y también cuando leía: ...los altos cielos que de vuestra divinidad divinamente con las estrellas os fortifican, y os hacen merecedora del merecimiento que merece la vuestra grandeza. Con estas razones perdía el pobre caballero el juicio, y desvelábase por entenderlas y desentrañarles el sentido, que no se lo sacara ni las entendiera el mesmo Aristóteles, si resucitara para sólo ello. No estaba muy bien con las heridas que don Belianís daba y recebía, porque se imaginaba que, por grandes maestros que le hubiesen curado, no dejaría de tener el rostro y todo el cuerpo lleno de cicatrices y señales. Pero, con todo, alababa en su autor aquel acabar su libro con la promesa de aquella inacabable aventura, y muchas veces le vino deseo de tomar la pluma y dalle fin al pie de la letra, como allí se promete; y sin duda alguna lo hiciera, y aun saliera con ello, si otros mayores y continuos pensamientos no se lo estorbaran. Tuvo muchas veces competencia con el cura de su lugar -que era hombre docto, graduado en Sigüenza-, sobre cuál había sido mejor caballero: Palmerín de Ingalaterra o Amadís de Gaula; mas maese Nicolás, barbero del mesmo pueblo, decía que ninguno llegaba al Caballero del Febo, y que si alguno se le podía comparar, era don Galaor, hermano de Amadís de Gaula, porque tenía muy acomodada condición para todo; que no era caballero melindroso, ni tan llorón como su hermano, y que en lo de la valentía no le iba en zaga. En resolución, él se enfrascó tanto en su letura, que se le pasaban las noches leyendo de claro en claro, y los días de turbio en turbio; y así, del poco dormir y del mucho leer, se le secó el celebro, de manera que vino a perder eljuicio. Llenósele la fantasía de todo aquello que leía en los libros, así de encantamentos como de pendencias, batallas, desafíos, heridas, requiebros, amores, tormentas y disparates imposibles; y asentósele de tal modo en la imaginación que era verdad toda aquella máquina de aquellas sonadas soñadas invenciones que leía, que para él no había otra historia más cierta en el mundo. Decía él que el Cid Ruy Díaz había sido muy buen caballero, pero que no tenía que ver con el Caballero de la Ardiente Espada, que de sólo un revés había partido por medio dos fieros y descomunales gigantes. Mejor estaba con Bernardo del Carpio, porque en Roncesvalles había muerto a Roldán el encantado, valiéndose de la industria de Hércules, cuando ahogó a Anteo, el hijo de la Tierra, entre los brazos. Decía mucho bien del gigante Morgante, porque, con ser de aquella generación gigantea, que todos son soberbios y descomedidos, él solo era afable y bien criado. Pero, sobre todos, estaba bien con Reinaldos de Montalbán, y más cuando le veía salir de su castillo y robar cuantos topaba, y cuando en allende robó aquel ídolo de Mahoma que era todo de oro, según dice su historia. Diera él, por dar una mano de coces al traidor de Galalón, al ama que tenía, y aun a su sobrina de añadidura.": |
El texto 4 es una receta de cocina. Tiene 1088 caracteres.
| > | texto4:="Bizcocho de las Carmelitas Descalzas de Sevilla. Se requieren 10 días para su elaboración, sin usar batidora ni frigorífico. Siempre hay que empezar el jueves. 1º día, jueves: se vierte el contenido del vaso en un recipiente mayor y se le añade 1 vaso de azúcar y otro de harina. No se mezcla. 2º día, viernes: se mezcla con una cuchara de madera. 3º día, sábado: no se toca. 4º día, domingo: no se toca. 5º día, lunes: se le añade un vaso de azúcar, otro de leche y otro de harina. No se mezcla. 6º día, martes: se mezcla todo bien con la cuchara de madera. 7º día, miércoles: no se toca. 8º día, jueves: no se toca. 9º día, viernes: no se toca. 10º día, sábado: se aparte de la masa tres vasos que se entregan a tres personas a las que se las desee suerte y salud, y al resto de la masa se le añade: 2 vasos de harina. 1 vaso de aceite. 1 vaso de leche. 1 vaso de nueces o almendras. 1 sobre de levadura. 2 huevos enteros. 1 manzana troceada. 1 pizca de sal. 1 pizca de vainilla. 1 pizca de canela. Se mezcla todo. Se mete al horno a 180º durante 30 ó 40 minutos. Dejar enfriar y comer.": |
El texto 5 se ha escrito sobre la marcha para probar caracteres poco frecuentes. Tiene 760 caracteres.
| > | texto5:="Necesito un texto en el que se prueben caracteres poco frecuentes como pueden ser /, *, #, o &. Es extraño encontrar estos elementos del lenguaje en textos comunes, aunque @, %, $ y € son bastante habituales. Es complicado situar paréntesis (aunque es más complicado introducir corchetes [ y ] o llaves { u }), pero al final de un modo u otro se pueden mencionar. Lo mismo ocurre con ~, ¬ o |, por ejemplo. Si hablamos de clasificaciones deportivas podemos ver símbolos como 1º, 2ª y similares. Los signos matemáticos están incluidos en nuestro alfabeto y son +, -, *, y /. Las potencias las podemos indicar mediante ^. También tenemos menor que < y mayor que >. Poco más puedo decir porque sólo falta por incluir la comilla simple ' y el guión bajo _. ¿¡FIN!?": |
Todas las curvas son de la forma ![]() en
en ![]() . En las que sea necesario se incluirá el punto base B.
. En las que sea necesario se incluirá el punto base B.
| > | a1:=3: b1:=1: n1:=4: #Curva 1 |
| > | a2:=3: b2:=1: n2:=5: #Curva 2 |
| > | a3:=-1: b3:=3: n3:=5: base3:=[2,3]: #Curva 3 |
| > | a4:=1: b4:=-2: n4:=5: #Curva 4 |
| > | a5:=-1: b5:=3: n5:=7: #Curva 5 |
| > | a6:=0: b6:=-2: n6:=7: #Curva 6 |
| > | a7:=-4: b7:=2: n7:=7: #Curva 7 |
| > | a8:=-4: b8:=2: n8:=11: #Curva 8 |
| > | a9:=1: b9:=3: n9:=11: base9:=[6,4]: #Curva 9 |
| > | a10:=-1: b10:=0: n10:=19: base10:=[5, 14]: #Curva 10 |
| > | a11:=1: b11:=-2: n11:=23: base11:=[17, 11]: #Curva 11 |
| > | a12:=0: b12:=-1: n12:=53: base12:=[31, 51]: #Curva 12 |
| > | a13:=-1: b13:=188: n13:=751: base13:=[565, 194]: #Curva 13 |
| > | a14:=-2: b14:=50: n14:=14831: base14:=[14619, 6880]: #Curva 14 |
| > | a15:=3101: b15:=2005: n15:=123456789059: base15:=[100098, 15890596801]: #Curva 15 |
| > | a16:=-2: b16:=50: n16:=1000000000000037: base16:=[29876406597393, 252423417455518]: #Curva 16 |
| > | a17:=4: b17:=4: n17:=29: #Curva 17 |
| > | ap192:=-3: bp192:=2455155546008943817740293915197451784769108058161191238065: np192:=6277101735386680763835789423207666416083908700390324961279: Bp192:=[602046282375688656758213480587526111916698976636884684818,174050332293622031404857552280219410364023488927386650641]: #Curva P-192 |
Algoritmo de Exponenciación Modular Rápida (AEMR)
Algoritmo eficiente para calcular múltiplos de un punto
Algoritmo para la suma de dos puntos de una Curva Elíptica
Aritmética de Curvas Elípticas
Comparativa entre ElGamal y Curvas Elípticas
Criptografía de Curva Elíptica
Criptosistema de Curvas Elípticas
Criterio para determinar raíces múltiples
Es una guía para profesionales y estudiantes, que trata la criptografía desde los principios y definiciones más básicos hasta otros más complejos. Presenta diferentes criptosistemas y sus aplicaciones en la vida real. También explica conceptos como el criptoanálisis y la firma digital. En particular, estudia con bastante detalle el criptosistema de curvas elípticas.
Se explican los fundamentos matemáticos sobre el Criptosistema de Curvas Elípticas. Además, se comenta el estado del arte de los algoritmos de implementación de este criptosistema y se detallan diferentes protocolos estandarizados de cifrado de clave pública, firma digital y generación de claves. Cabe destacar el capítulo 3, en el que se define la aritmética de curvas elípticas.
Trata sobre la aritmética de la teoría de números y sus aplicaciones en criptografía. Introduce las curvas elípticas desde un punto de vista matemático analizando su eficiencia. Incluye ejercicios resueltos. Requiere tener conocimientos matemáticos.
La temática es muy amplia en lo que a criptografía se refiere. Analiza en profundidad una gran variedad de métodos de cifrado y descifrado, criptoanálisis y firma digital. En el caso de las curvas elípticas, les dedica un capítulo completo. Requiere tener amplios conocimientos matemáticos y criptográficos.
Realiza un sondeo de los principios de la criptografía y la seguridad en redes. Está dirigido a estudiantes de criptografía, seguridad informática y seguridad en redes.
Soluciones de los ejercicios
Utiliza la función GeneraClaveGamal de la librería CurvasElipt para crear claves de 5, 10 y 15 dígitos:
| > | clave1:=GeneraClaveGamal(5, priv1); |
| (11.1.1) |
| > | priv1; |
| (11.1.2) |
| > | clave2:=GeneraClaveGamal(10, priv2); |
| (11.1.3) |
| > | priv2; |
| (11.1.4) |
| > | clave3:=GeneraClaveGamal(15, priv3); |
| (11.1.5) |
| > | priv3; |
| (11.1.6) |
A continuación, comprueba los resultados anteriores aplicando las fórmulas comentadas en el apartado anterior:
Aplicando los criterios del apartado 3.2, se obtiene o siguiente:
| > | clave1[2]&^priv1[2] mod priv1[1]; |
| (11.1.7) |
Comprueba que el resultado coincide:
| > | is(%=clave1[3]); |
| (11.1.8) |
Procede del mismo modo con los otros dos casos:
| > | clave2[2]&^priv2[2] mod priv2[1]; |
| (11.1.9) |
| > | is(%=clave2[3]); |
| (11.1.10) |
| > | clave3[2]&^priv3[2] mod priv3[1]; |
| (11.1.11) |
| > | is(%=clave3[3]); |
| (11.1.12) |
Supón dos usuarios, Alicia y Bob, que quieren enviarse mensajes de modo seguro. Sigue el esquema anteriormente explicado, crea un mensaje de texto y cífralo para que Bob se lo envíe a Alicia. Una vez que Bob lo haya recibido, desencriptalo para comprobar que el resultado es correcto. Se recomienda la utilización de la función para cifrar y descifrar ElGamal.
En primer lugar, se generan las claves pública y privada para Alicia y Bob. Tomaremos, por ejemplo, una clave de 5 dígitos.
| > | clavePúblicaAlicia:=GeneraClaveGamal(5, privadaAlicia); |
| (11.2.1) |
| > | clavePúblicaBob:=GeneraClaveGamal(5, privadaBob); |
| (11.2.2) |
Sus claves privadas serán:
| > | privadaAlicia; |
| (11.2.3) |
| > | privadaBob; |
| (11.2.4) |
Bob, quiere enviar el siguiente mensaje a Alicia:
| > | mensaje:="¡Hola! ¿Qué tal? Estoy realizando una prueba del criptosistema de ElGamal."; |
| (11.2.5) |
A continuación Bob cifra el mensaje con la clave pública de Alicia (como alfabeto utilizaremos la variable castellano, contenida en la librería CurvasElipt):
| > | criptoBob:=ElGamal(mensaje,castellano,clavePúblicaAlicia); |
| (11.2.6) |
Cuando Alicia lo recibe, lo desencripta con su clave privada y puede leer el mensaje en claro:
| > | ElGamal(criptoBob,castellano,privadaAlicia); |
| (11.2.7) |
Decide cuál es la lóngitud máxima en la que se se deben partir los bloques de un mensaje para que los mensajes se representen como un elemento de ℤ67 de modo único. Utiliza como alfabeto [A, E, N, O, P, S]:
Generamos el alfabeto y lo guardamos en una variable:
| > | alfabeto:="AENOPS"; |
| (11.3.1) |
Establecemos p y r, el tamaño del alfabeto:
| > | p:=67; |
| (11.3.2) |
| > | r:=length(alfabeto); |
| (11.3.3) |
La longitud máxima de los bloques viene dada por:
| > | (r^(l+1) - 1)/(r-1) <= p; |
| (11.3.4) |
Despejamos r en la ecuación y obtenemos lo siguiente:
| > | r^(l+1)<=336; |
| (11.3.5) |
Aplicamos logaritmos para hallar el valor de l:
| > | l+1 <= log[r](336); |
| (11.3.6) |
Tomamos la parte entera para obtener el tamaño máximo de bloque.
| > | l <= floor(log[r](336)-1); |
| (11.3.7) |
Por lo que el tamaño máximo de bloque será 2.
Genera claves de ElGamal de 5, 7 y 9 dígitos. A continuación realiza el criptoanálisis de la clave con la función LogaritmoDiscreto, evaluando los tiempos de ejecución mediante la función time de Maple.
Generamos la clave de 5 dígitos:
| > | clave1:=GeneraClaveGamal(5, privada1); |
| (11.4.1) |
Tomamos el tiempo inicial y aplicamos la función LogaritmoDiscreto con la clave generada:
| > | t:=time(); |
| (11.4.2) |
| > | resul1:=LogaritmoDiscreto(clave1[2],clave1[1],clave1[3]); |
| (11.4.3) |
Mostramos el tiempo que ha tardado el criptoanálisis:
| > | time()-t; |
| (11.4.4) |
Comprobamos que el resultado del criptoanálisis es correcto:
| > | is(resul1=privada1[2]); |
| (11.4.5) |
Procedemos de igual modo con las claves de 7 y 9 dígitos:
| > | clave2:=GeneraClaveGamal(7, privada2); |
| (11.4.6) |
| > | t:=time(); |
| (11.4.7) |
| > | resul2:=LogaritmoDiscreto(clave2[2],clave2[1],clave2[3]); |
| (11.4.8) |
| > | time()-t; |
| (11.4.9) |
| > | is(resul2=privada2[2]); |
| (11.4.10) |
| > | clave3:=GeneraClaveGamal(9, privada3); |
| (11.4.11) |
| > | t:=time(); |
| (11.4.12) |
| > | resul3:=LogaritmoDiscreto(clave3[2],clave3[1],clave3[3]); |
| (11.4.13) |
| > | time()-t; |
| (11.4.14) |
| > | is(resul3=privada3[2]); |
| (11.4.15) |
Determina si las siguientes cúbicas definen una curva elíptica en los cuerpos que se indican. Para aquellos casos en los que sea curva elíptica, halla todos los puntos de la curva. Recuerda que debes tener en cuenta el punto del infinito θE. Comprueba los resultados con la función ListarPuntos de la librería CurvasElipt.
a) ![]() con =
con = ![]() y
y ![]()
b) ![]() con con en
con con en ![]() y
y ![]()
c) ![]() con en
con en ![]() y
y ![]()
Para resolver cada apartado, aplicamos la propiedad explicada en el apartado 4.3 después de transformar las funciones a la forma ![]() :
:
Apartado a) ![]()
| > | Factor(x*(x+10)*(x+35))mod 5; |
| (11.5.1) |
En ![]() obviamente, x = 0 es solución triple de la cúbica. Por lo que tiene raíces múltiples y no es una curva elíptica.
obviamente, x = 0 es solución triple de la cúbica. Por lo que tiene raíces múltiples y no es una curva elíptica.
Apartado a) ![]()
| > | Factor(x*(x+10)*(x+35))mod 7; |
| (11.5.2) |
No ha sido necesario aplicar el discriminante ya que x = 0 es solución doble (múltiple) de la cúbica. Por lo que no es curva elíptica en ![]() .
.
Apartado b) ![]()
| > | Factor(x^3 - 2) mod 5; |
| (11.5.3) |
| > | discriminante:=(4*0^3 + 27 * 3^2) mod 5; |
| (11.5.4) |
| > | is(discriminante = 0); |
| (11.5.5) |
En este caso sólo tiene una posible raíz en ![]() , que es x = 3, y el discriminante es distinto de 0, por lo que la cúbica es curva elíptica.
, que es x = 3, y el discriminante es distinto de 0, por lo que la cúbica es curva elíptica.
Vamos a calcular los puntos de la curva. Para ello, en primer lugar vemos cuales son los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to 5-1 do cuadrados:={op(cuadrados),i&^2 mod 5}; end do; |
| (11.5.6) |
Seguidamente calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados:
y comprobamos si son cuadrados:
| > | for i from 0 to 5-1 do
raiz:=[i,(i^3 - 2) mod 5]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (11.5.7) |
En vista de los resultados tenemos que f(1), f(2) y f(3) son cuadrados. Por tanto (1, ± ![]() ) = (1, ±2), (2, ±
) = (1, ±2), (2, ± ![]() ) = (2, ±1) y (3, ±
) = (2, ±1) y (3, ± ![]() ) = (3, ±0) son los únicos puntos de la curva en
) = (3, ±0) son los únicos puntos de la curva en ![]() ×
×![]() tiene 6 puntos: E(
tiene 6 puntos: E(![]() ) = {(1, 2), (1, 3), (2, 1), (2, 4), (3, 0), θE}
) = {(1, 2), (1, 3), (2, 1), (2, 4), (3, 0), θE}
A continuación, por medio de la función ListarPuntos comprobamos los resultados obteniendo la lista de los puntos de la curva y su representación gráfica:
| > | a:=0: b:=-2: n:=5: |
| > | ListarPuntos(a,b,n,true); |
 |
|
| (11.5.8) |
Apartado b) ![]()
| > | Factor(x^3 - 2) mod 7; |
| (11.5.9) |
| > | discriminante:=(4*0^3 + 27 * 5^2) mod 7; |
| (11.5.10) |
| > | is(discriminante = 0); |
| (11.5.11) |
En ![]() no tiene raíces. Por ello el discriminante es distinto de 0 y la cúbica es curva elíptica.
no tiene raíces. Por ello el discriminante es distinto de 0 y la cúbica es curva elíptica.
Vamos a calcular los puntos de la curva. Para ello, en primer lugar vemos cuales son los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to 7-1 do cuadrados:={op(cuadrados),i&^2 mod 7}; end do; |
| (11.5.12) |
Seguidamente calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados:
y comprobamos si son cuadrados:
| > | for i from 0 to 7-1 do
raiz:=[i,(i^3 - 2) mod 7]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (11.5.13) |
En vista de los resultados tenemos que f(1), f(2) y f(3) son cuadrados. Por tanto (3, ± ![]() ) = (3, ±2), (5, ±
) = (3, ±2), (5, ± ![]() ) = (5, ±2) y (6, ±
) = (5, ±2) y (6, ± ![]() ) = (6, ±2) son los únicos puntos de la curva en
) = (6, ±2) son los únicos puntos de la curva en ![]() ×
×![]() tiene 7 puntos: E(
tiene 7 puntos: E(![]() ) = {(3, 2), (3, 5), (5, 2), (5, 5), (6, 2), (6, 5), θE}
) = {(3, 2), (3, 5), (5, 2), (5, 5), (6, 2), (6, 5), θE}
A continuación, por medio de la función ListarPuntos comprobamos los resultados obteniendo la lista de los puntos de la curva y su representación gráfica:
| > | a:=0: b:=-2: n:=7: |
| > | ListarPuntos(a,b,n,true); |
 |
|
| (11.5.14) |
Apartado c) ![]()
| > | Factor((x-5)*(x-10)*(x-2)) mod 5; |
| (11.5.15) |
| > | discriminante:=(4*0^3 + 27 * 0^2) mod 7; |
| (11.5.16) |
| > | is(discriminante = 0); |
| (11.5.17) |
En este caso en ![]() hay una raíz múltiple x = 0. Por ello el discriminante es 0 y la cúbica no es curva elíptica.
hay una raíz múltiple x = 0. Por ello el discriminante es 0 y la cúbica no es curva elíptica.
Apartado c) ![]()
| > | Factor((x-5)*(x-10)*(x-2)) mod 7; |
| (11.5.18) |
| > | discriminante:=(4*3^3 + 27 * 2^2) mod 7; |
| (11.5.19) |
| > | is(discriminante = 0); |
| (11.5.20) |
En este caso tanía 3 raíces diferentes en ![]() (x = 2, x = 5 y x = 3) y el discriminante es distinto de 0, por lo que la cúbica es curva elíptica.
(x = 2, x = 5 y x = 3) y el discriminante es distinto de 0, por lo que la cúbica es curva elíptica.
Vamos a calcular los puntos de la curva. Para ello, en primer lugar vemos cuales son los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to 7-1 do cuadrados:={op(cuadrados),i&^2 mod 7}; end do; |
| (11.5.21) |
Seguidamente calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados:
y comprobamos si son cuadrados:
| > | for i from 0 to 7-1 do
raiz:=[i,(i-5)*(i-10)*(i-2) mod 7]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (11.5.22) |
En vista de los resultados tenemos que f(2), f(3) y f(5) son raíces y cuadrados. Por tanto (2, ± ![]() ) = (2, ±0), (3, ±
) = (2, ±0), (3, ± ![]() ) = (3, ±0) y (5, ±
) = (3, ±0) y (5, ± ![]() ) = (5, ±0) son los únicos puntos de la curva en
) = (5, ±0) son los únicos puntos de la curva en ![]() ×
×![]() tiene 4 puntos: E(
tiene 4 puntos: E(![]() ) = { (2, 0), (3, 0), (5, 0), θE}
) = { (2, 0), (3, 0), (5, 0), θE}
A continuación, por medio de la función ListarPuntos comprobamos los resultados obteniendo la lista de los puntos de la curva y su representación gráfica. Pero antes, debemos obtener la forma canónica de la curva mediante un cambio de variable para sustituir el término ![]() :
:
| > | cúbica:=expand((x-5)*(x-10)*(x-2)) mod 7; |
| (11.5.23) |
Realizaremos el cambio de variable ![]() y lo realizamos del siguiente modo en
y lo realizamos del siguiente modo en ![]() :
:
| > | 4/3 mod 7; |
| (11.5.24) |
| > | canónica:=expand(subs(x=z-6, cúbica)) mod 7; |
| (11.5.25) |
Por lo tanto, la forma canónica que obtenemos es ![]() . Comprobamos los resultados con la función ListarPuntos:
. Comprobamos los resultados con la función ListarPuntos:
| > | a:=0: b:=6: n:=7: |
| > | ListarPuntos(0,6,7,true); |
 |
|
| (11.5.26) |
Vemos que los puntos no coinciden, pero debemos recordar que hemos realizado el cambio de variable ![]() mod 7. Por lo que debemos aplicar este cambio de variable a los puntos obtenidos:
mod 7. Por lo que debemos aplicar este cambio de variable a los puntos obtenidos:
Por lo tanto, con el cambio de variable tenemos que los puntos son { (2, 0), (3, 0), (5, 0), θE} por lo que podemos confirmar que el resultado es correcto.
Calcula las sumas entre todos los puntos de la curva ![]()
![]() . Comprueba los resultados con la función
TablaSumas de la librería CurvasElipt.
. Comprueba los resultados con la función
TablaSumas de la librería CurvasElipt.
Creamos las variables que representarán la curva:
| > | a:=-4: b:=2: n:=11: |
En primer lugar, listamos todos los puntos de la curva. Para ello, calculamos los cuadrados de ![]() :
:
| > | cuadrados:={};
for i from 0 to n-1 do cuadrados:={op(cuadrados),i&^2 mod n}; end do; |
| (11.6.1) |
A continuación calculamos cuántas raíces tiene la cúbica en ![]() y comprobamos si son cuadrados:
y comprobamos si son cuadrados:
| > | for i from 0 to n-1 do
raiz:=[i,(i^3+a*i+b) mod n]; Es_Cuadrado:=is(raiz[2] in cuadrados); end do; |
| (11.6.2) |
En vista de los resultados tenemos que f(7), f(8) y f(10) son cuadrados. Por tanto (7, ± ![]() ) = (7, ±3), (8, ±
) = (7, ±3), (8, ± ![]() ) = (8, ±3) y (10, ±
) = (8, ±3) y (10, ± ![]() ) = (10, ±4) son los únicos puntos de la curva en
) = (10, ±4) son los únicos puntos de la curva en ![]() ×
×![]() . Entonces
. Entonces ![]() en
en ![]() tiene 4 puntos: E(
tiene 4 puntos: E(![]() ) = {(7, 3), (7, 8), (8, 3), (8, 8), (10, 4), (10, 7), θE}
) = {(7, 3), (7, 8), (8, 3), (8, 8), (10, 4), (10, 7), θE}
Y comprobamos que es correcto mediante la función ListarPuntos de la librería CurvasElipt:
| > | lista:=ListarPuntos(a,b,n,true); |
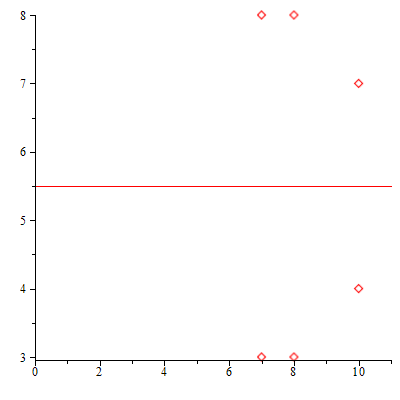 |
|
| (11.6.3) |
Conociendo los puntos, procedemos a realizar las sumas entre ellos. En primer lugar, asignamos los puntos a variables para facilitar los cálculos:
| > | P:=[7,3]: Q:=[7,8]: R:=[8,3]: S:=[8,8]: T:=[10,4]: U:=[10,7]: V:=infinity: |
Vamos a calcular P+P:
| > | mP_P:=((3*(P[1]^2)+a)/(2*P[2])) mod n;
x:=mP_P^2-P[1]-P[1] mod n; y:=mP_P*(P[1]-x)-P[2] mod n; P_P:=[x,y] mod n; |
| (11.6.4) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,P); |
| (11.6.5) |
Vamos a calcular P+Q:
| > | mP_Q:=(Q[2]-P[2])/(Q[1]-P[1]) mod n;
x:=mP_Q^2-P[1]-Q[1] mod n; y:=mP_Q*(P[1]-x)-P[2] mod n; P_Q:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (11.6.6) |
En este caso, al calcular mP_Q se produce una división por 0, por lo que P+Q = θE
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,Q); |
| (11.6.7) |
Vamos a calcular P+R:
| > | mP_R:=(R[2]-P[2])/(R[1]-P[1]) mod n;
x:=mP_R^2-P[1]-R[1] mod n; y:=mP_R*(P[1]-x)-P[2] mod n; P_R:=[x,y] mod n; |
| (11.6.8) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,R); |
| (11.6.9) |
Vamos a calcular P+S:
| > | mP_S:=(S[2]-P[2])/(S[1]-P[1]) mod n;
x:=mP_S^2-P[1]-S[1] mod n; y:=mP_S*(P[1]-x)-P[2] mod n; P_S:=[x,y] mod n; |
| (11.6.10) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,S); |
| (11.6.11) |
Vamos a calcular P+T:
| > | mP_T:=(T[2]-P[2])/(T[1]-P[1]) mod n;
x:=mP_T^2-P[1]-T[1] mod n; y:=mP_T*(P[1]-x)-P[2] mod n; P_T:=[x,y] mod n; |
| (11.6.12) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,T); |
| (11.6.13) |
Vamos a calcular P+U:
| > | mP_U:=(U[2]-P[2])/(U[1]-P[1]) mod n;
x:=mP_U^2-P[1]-U[1] mod n; y:=mP_U*(P[1]-x)-P[2] mod n; P_U:=[x,y] mod n; |
| (11.6.14) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,U); |
| (11.6.15) |
Vamos a calcular P+V:
Para este caso tenemos que P + θE := P = [7,3]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,P,V); |
| (11.6.16) |
Vamos a calcular Q+Q:
| > | mQ_Q:=((3*(Q[1]^2)+a)/(2*Q[2])) mod n;
x:=mQ_Q^2-Q[1]-Q[1] mod n; y:=mQ_Q*(Q[1]-x)-Q[2] mod n; Q_Q:=[x,y] mod n; |
| (11.6.17) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,Q); |
| (11.6.18) |
Vamos a calcular Q+R:
| > | mQ_R:=(R[2]-Q[2])/(R[1]-Q[1]) mod n;
x:=mQ_R^2-P[1]-R[1] mod n; y:=mQ_R*(Q[1]-x)-Q[2] mod n; Q_R:=[x,y] mod n; |
| (11.6.19) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,R); |
| (11.6.20) |
Vamos a calcular Q+S:
| > | mQ_S:=(S[2]-Q[2])/(S[1]-Q[1]) mod n;
x:=mQ_S^2-P[1]-S[1] mod n; y:=mQ_S*(Q[1]-x)-Q[2] mod n; Q_S:=[x,y] mod n; |
| (11.6.21) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,S); |
| (11.6.22) |
Vamos a calcular Q+T:
| > | mQ_T:=(T[2]-Q[2])/(T[1]-Q[1]) mod n;
x:=mQ_T^2-P[1]-T[1] mod n; y:=mQ_T*(Q[1]-x)-Q[2] mod n; Q_T:=[x,y] mod n; |
| (11.6.23) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,T); |
| (11.6.24) |
Vamos a calcular Q+U:
| > | mQ_U:=(U[2]-Q[2])/(U[1]-Q[1]) mod n;
x:=mQ_U^2-P[1]-U[1] mod n; y:=mQ_U*(Q[1]-x)-Q[2] mod n; Q_U:=[x,y] mod n; |
| (11.6.25) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,U); |
| (11.6.26) |
Vamos a calcular Q+V:
Para este caso tenemos que Q + θE := Q = [7,8]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,Q,V); |
| (11.6.27) |
Vamos a calcular R+R:
| > | mR_R:=((3*(R[1]^2)+a)/(2*R[2])) mod n;
x:=mR_R^2-R[1]-R[1] mod n; y:=mR_R*(R[1]-x)-R[2] mod n; R_R:=[x,y] mod n; |
| (11.6.28) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,R,R); |
| (11.6.29) |
Vamos a calcular R+S:
| > | mR_S:=(S[2]-R[2])/(S[1]-R[1]) mod n;
x:=mR_S^2-R[1]-S[1] mod n; y:=mR_S*(R[1]-x)-R[2] mod n; R_S:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (11.6.30) |
En este caso, al calcular mR_S se produce una división por 0, por lo que R+S = θE
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,R,S); |
| (11.6.31) |
Vamos a calcular R+T:
| > | mR_T:=(T[2]-R[2])/(T[1]-R[1]) mod n;
x:=mR_T^2-R[1]-T[1] mod n; y:=mR_T*(R[1]-x)-R[2] mod n; R_T:=[x,y] mod n; |
| (11.6.32) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,R,T); |
| (11.6.33) |
Vamos a calcular R+U:
| > | mR_U:=(U[2]-R[2])/(U[1]-R[1]) mod n;
x:=mR_U^2-R[1]-U[1] mod n; y:=mR_U*(R[1]-x)-R[2] mod n; R_U:=[x,y] mod n; |
| (11.6.34) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,R,U); |
| (11.6.35) |
Vamos a calcular R+V:
Para este caso tenemos que R + θE := R = [8,3]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,R,V); |
| (11.6.36) |
Vamos a calcular S+S:
| > | mS_S:=((3*(S[1]^2)+a)/(2*S[2])) mod n;
x:=mS_S^2-S[1]-S[1] mod n; y:=mS_S*(S[1]-x)-S[2] mod n; S_S:=[x,y] mod n; |
| (11.6.37) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,S,S); |
| (11.6.38) |
Vamos a calcular S+T:
| > | mS_T:=(T[2]-S[2])/(T[1]-S[1]) mod n;
x:=mS_T^2-S[1]-T[1] mod n; y:=mS_T*(S[1]-x)-S[2] mod n; S_T:=[x,y] mod n; |
| (11.6.39) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,S,T); |
| (11.6.40) |
Vamos a calcular S+U:
| > | mS_U:=(U[2]-S[2])/(U[1]-S[1]) mod n;
x:=mS_U^2-S[1]-U[1] mod n; y:=mS_U*(S[1]-x)-S[2] mod n; S_U:=[x,y] mod n; |
| (11.6.41) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,S,U); |
| (11.6.42) |
Vamos a calcular S+V:
Para este caso tenemos que S + θE := S = [8,8]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,S,V); |
| (11.6.43) |
Vamos a calcular T+T:
| > | mT_T:=((3*(T[1]^2)+a)/(2*T[2])) mod n;
x:=mT_T^2-T[1]-T[1] mod n; y:=mT_T*(T[1]-x)-T[2] mod n; T_T:=[x,y] mod n; |
| (11.6.44) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,T,T); |
| (11.6.45) |
Vamos a calcular T+U:
| > | mT_U:=(U[2]-T[2])/(U[1]-T[1]) mod n;
x:=mT_U^2-T[1]-U[1] mod n; y:=mT_U*(T[1]-x)-T[2] mod n; T_U:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (11.6.46) |
En este caso, al calcular mT_U se produce una división por 0, por lo que T+U = θE
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,T,U); |
| (11.6.47) |
Vamos a calcular T+V:
Para este caso tenemos que T + θE := T = [10,4]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,T,V); |
| (11.6.48) |
Vamos a calcular U+U:
| > | mU_U:=((3*(U[1]^2)+a)/(2*U[2])) mod n;
x:=mU_U^2-U[1]-U[1] mod n; y:=mU_U*(U[1]-x)-U[2] mod n; U_U:=[x,y] mod n; |
| (11.6.49) |
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,U,U); |
| (11.6.50) |
Vamos a calcular U+V:
Para este caso tenemos que U + θE := U = [10,7]
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,U,V); |
| (11.6.51) |
Vamos a calcular V+V:
Debido a que V es el punto en el infinito θE, tenemos que V+V = θE
Comprobamos el resultado pormedio de la función SumaPuntos de la librería CurvasElipt:
| > | SumaPuntos(a,b,n,V,V); |
| (11.6.52) |
Por último, podemos comprobar todos los resultados con la función TablaSumas:
| > | TablaSumas(a,b,n); |
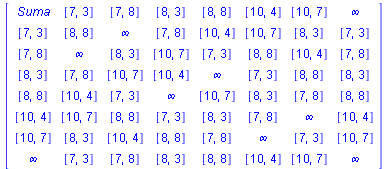 |
(11.6.53) |
Calcula los órdenes de los puntos P = (6,4) y Q = (1,7) de la curva elíptica ![]()
![]() .
.
En primer lugar asignamos los parámetros de la curva y los puntos a variables:
| > | a:=1: b:=3: n:=11: P:=[6,4]: Q:=[1,7]: |
Para calcular el orden de P = (6,4), vamos a calcular sus múltiplos hasta encontrar el número k que cumpla ![]()
En primer lugar calculamos 2P = P+P:
| > | mP_2P:=((3*(P[1]^2)+a)/(2*P[2])) mod n;
x:=mP_2P^2-P[1]-P[1] mod n; y:=mP_2P*(P[1]-x)-P[2] mod n; P_2P:=[x,y] mod n; |
| (11.7.1) |
Vemos que 2P = (4,4). Por no ser ![]() calculamos 3P = 2P+P:
calculamos 3P = 2P+P:
| > | mP_3P:=(P_2P[2]-P[2])/(P_2P[1]-P[1]) mod n;
x:=mP_3P^2-P[1]-P_2P[1] mod n; y:=mP_3P*(P[1]-x)-P[2] mod n; P_3P:=[x,y] mod n; |
| (11.7.2) |
Vemos que 3P = (1,7). Por no ser ![]() calculamos 4P = 3P+P:
calculamos 4P = 3P+P:
| > | mP_4P:=(P_3P[2]-P[2])/(P_3P[1]-P[1]) mod n;
x:=mP_4P^2-P[1]-P_3P[1] mod n; y:=mP_4P*(P[1]-x)-P[2] mod n; P_4P:=[x,y] mod n; |
| (11.7.3) |
Vemos que 4P = (7,1). Por no ser ![]() calculamos 5P = 4P+P:
calculamos 5P = 4P+P:
| > | mP_5P:=(P_4P[2]-P[2])/(P_4P[1]-P[1]) mod n;
x:=mP_5P^2-P[1]-P_4P[1] mod n; y:=mP_5P*(P[1]-x)-P[2] mod n; P_5P:=[x,y] mod n; |
| (11.7.4) |
Vemos que 5P = (7,10). Por no ser ![]() calculamos 6P = 5P+P:
calculamos 6P = 5P+P:
| > | mP_6P:=(P_5P[2]-P[2])/(P_5P[1]-P[1]) mod n;
x:=mP_6P^2-P[1]-P_5P[1] mod n; y:=mP_6P*(P[1]-x)-P[2] mod n; P_6P:=[x,y] mod n; |
| (11.7.5) |
Vemos que 6P = (1,4). Por no ser ![]() calculamos 7P = 6P+P:
calculamos 7P = 6P+P:
| > | mP_7P:=(P_6P[2]-P[2])/(P_6P[1]-P[1]) mod n;
x:=mP_7P^2-P[1]-P_6P[1] mod n; y:=mP_7P*(P[1]-x)-P[2] mod n; P_7P:=[x,y] mod n; |
| (11.7.6) |
Vemos que 7P = (4,7). Por no ser ![]() calculamos 8P = 7P+P:
calculamos 8P = 7P+P:
| > | mP_8P:=(P_7P[2]-P[2])/(P_7P[1]-P[1]) mod n;
x:=mP_8P^2-P[1]-P_7P[1] mod n; y:=mP_8P*(P[1]-x)-P[2] mod n; P_8P:=[x,y] mod n; |
| (11.7.7) |
Vemos que 8P = (6,7). Por no ser ![]() calculamos 9P = 8P+P:
calculamos 9P = 8P+P:
| > | mP_9P:=(P_8P[2]-P[2])/(P_8P[1]-P[1]) mod n;
x:=mP_9P^2-P[1]-P_8P[1] mod n; y:=mP_9P*(P[1]-x)-P[2] mod n; P_9P:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (11.7.8) |
En este caso, al calcular mP_9P se produce una división por 0, por lo que 9P = 8P+P = θE y el orden del punto P = (6,4) es 9.
Podemos comprobar que los cálculos anteriores son correctos con la función MúltiploPunto de la librería CurvasElipt:
| > | i:=1:
while MúltiploPunto(a,b,n,i,P) <> infinity do i:=i+1; od: i; |
| (11.7.9) |
Por lo tanto, el orden del punto P = (6,4) de la curva elíptica ![]()
![]() es 9.
es 9.
Para calcular el orden de Q = (1,7), vamos a calcular sus múltiplos hasta encontrar el número k que cumpla ![]()
En primer lugar calculamos 2Q = Q+Q:
| > | mQ_2Q:=((3*(Q[1]^2)+a)/(2*Q[2])) mod n;
x:=mQ_2Q^2-Q[1]-Q[1] mod n; y:=mQ_2Q*(Q[1]-x)-Q[2] mod n; Q_2Q:=[x,y] mod n; |
| (11.7.10) |
Vemos que 2Q = (1,4). Por no ser ![]() calculamos 3Q = 2Q+Q:
calculamos 3Q = 2Q+Q:
| > | mQ_3Q:=(Q_2Q[2]-Q[2])/(Q_2Q[1]-Q[1]) mod n;
x:=mQ_3Q^2-Q[1]-Q_2Q[1] mod n; y:=mQ_3Q*(Q[1]-x)-Q[2] mod n; Q_3Q:=[x,y] mod n; |
| Error, numeric exception: division by zero | |
| (11.7.11) |
En este caso, al calcular mQ_3Q se produce una división por 0, por lo que 3Q = 2Q+Q = θE y el orden del punto Q = (1,7) es 3.
Podemos comprobar que los cálculos anteriores son correctos con la función MúltiploPunto de la librería CurvasElipt:
| > | i:=1:
while MúltiploPunto(a,b,n,i,[1,7]) <> infinity do i:=i+1; od: i; |
| (11.7.12) |
Por lo tanto, el orden del punto Q = (3,0) de la curva elíptica ![]()
![]() es 2.
es 2.
Determina las cotas inferior y superior para el número de puntos de una curva elíptica cuando:
Aplicamos las cotas definitas en el apartado 5.6. Teorema de Hasse:
(a) = ![]()
| > | evalf((23+1)-2*23^(1/2)) <= N; N <= evalf((23+1)+2*23^(1/2)); |
| (11.8.1) |
Por tanto, el número de puntos de una curva elíptica en ![]() está en el rango 15..33.
está en el rango 15..33.
(b) = ![]()
| > | evalf((51+1)-2*51^(1/2)) <= N; N <= evalf((51+1)+2*51^(1/2)); |
| (11.8.2) |
Por tanto, el número de puntos de una curva elíptica en ![]() está en el rango 38..66.
está en el rango 38..66.
(c) = ![]()
| > | evalf((127+1)-2*127^(1/2)) <= N; N <= evalf((127+1)+2*127^(1/2)); |
| (11.8.3) |
Por tanto, el número de puntos de una curva elíptica en ![]() está en el rango 106..150.
está en el rango 106..150.
¿Pueden existir curvas elípticas sobre ![]() con 31 puntos? ¿Y con 4?
con 31 puntos? ¿Y con 4?
Calculamos las cotas para ![]() :
:
| > | evalf((11+1)-2*11^(1/2)) <= N; N <= evalf((11+1)+2*11^(1/2)); |
| (11.8.4) |
Según las cotas, el número de puntos de una curva elíptica en ![]() está en el rango 6..18. Por lo tanto, no podrá tener curvas con 31 puntos ni con 4 puntos, dado que estos valores no se encuentran entre las cotas.
está en el rango 6..18. Por lo tanto, no podrá tener curvas con 31 puntos ni con 4 puntos, dado que estos valores no se encuentran entre las cotas.
Aplica el algoritmo anterior para calcular 11P, siendo P = (1,5) un punto de la curva eliptica E(![]() ):
): ![]() . Comprueba el resultado mediante la función MúltiploPunto de la librería CurvasElipt.
. Comprueba el resultado mediante la función MúltiploPunto de la librería CurvasElipt.
En primer lugar, representamos los parámetros de la curva mediante variables:
| > | a:=4: b:=20: n:=29: P:=[1,5]: k:=11: |
1. Vemos que P no es θE ni k es 0, por lo que definimos s (el valor de la suma) y c (los múltiplos de P con escalar potencia de 2):
| > | s:=infinity; c:=P; |
| (11.9.1) |
2. Definimos q (cociente de la división euclídea de k entre 2) y r (resto de la división euclídea de k entre 2):
| > | q:=iquo(abs(k),2,'r');
r; |
| (11.9.2) |
Como r = 1 realizamos la asignación s := c.
| > | s:=c; |
| (11.9.3) |
3. Como q es distinto de 0, tenemos que seguir haciendo los siguientes cálculos:
| > | c:=SumaPuntos(a,b,n,c,c);
q:=iquo(abs(q),2,'r'); r; |
| (11.9.4) |
Tenemos que r = 1, por lo que realizamos la asignación s := s + c.
| > | s:=SumaPuntos(a,b,n,s,c); |
| (11.9.5) |
Como q es distinto de 0, seguimos realizantdo los cálculos:
| > | c:=SumaPuntos(a,b,n,c,c);
q:=iquo(abs(q),2,'r'); r; |
| (11.9.6) |
Como r = 0, esta vez no tenemos que realizar la asicnación s := c y, como q es distinto de 0, seguimos realizantdo los cálculos:
| > | c:=SumaPuntos(a,b,n,c,c);
q:=iquo(abs(q),2,'r'); r; |
| (11.9.7) |
Tenemos que r = 1, por lo que realizamos la asignación s := s + c.
| > | s:=SumaPuntos(a,b,n,s,c); |
| (11.9.8) |
Por último, como q = 0, devolvemos s, ya que contiene 6P:
| > | s; |
| (11.9.9) |
Comprobamos el resultado mediante la función MúltiploPunto de la librería CurvasElipt y que utiliza el algoritmo eficiente para calcular múltiplos de un punto:
| > | MúltiploPunto(a,b,n,k,P); |
| (11.9.10) |
Vemos que los resultados coinciden. Para ver de una manera más clara el funcionamiento del algoritmo, lo podemos resumir en una tabla (i = nº de iteración; q = cociente de la división euclídea; r = resto de la división euclídea; s = valor de la suma; c = múltiplos de P con escalar potencia de 2):
i |
q |
r |
s |
c |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Dados los puntos B = (29876406597393, 252423417455518) y P = (![]() ) de la curva
) de la curva ![]() en
en ![]() que puedes encontrar en el capítulo Recursos como #Curva16, calcula el valor de k tal que kB = P. Comprueba el resultado mediante la función LogaritmoPunto de la librería CurvasElipt.
que puedes encontrar en el capítulo Recursos como #Curva16, calcula el valor de k tal que kB = P. Comprueba el resultado mediante la función LogaritmoPunto de la librería CurvasElipt.
En primer lugar representamos los parámetros de la curva mediante variables:
| > | a:=-2: b:=50: n:=1000000000000037: B:=[29876406597393, 252423417455518]: P:=[293001176497636, 858156641820468]: |
A continuación calculamos los múltiplos del punto B mediante un bucle while y la función MúltiploPunto de la librería CurvasElipt, hasta encontrar el valor de k que satisfaga kB = P:
| > | i:=0: encontrado:=false:
while (i < n) and (not encontrado) do múltiplo:=MúltiploPunto(a,b,n,i,B): if múltiplo = P then encontrado:=true: k:=i: end if: i:=i+1: end do: múltiplo:=múltiplo; k:=k; |
| (11.10.1) |
Comprobamos que el valor de la variable "múltiplo" coincide con P:
| > | is(múltiplo = P); |
| (11.10.2) |
Por último, comprobamos el resultado mediante la función LogaritmoPunto de la librería CurvasElipt:que el valor de k es correcto:
| > | Log:=LogaritmoPunto(a,b,n,B,P); |
| (11.10.3) |
Vemos que el valor obtenido coincide con k:
| > | is(Log = k); |
| (11.10.4) |
Utiliza las funciones TextoPunto y PuntoTexto de la librería CurvasElipt para representar los símbolos del alfabeto [A,B,C,D,E,F]. Para ello utiliza la curva ![]() en
en ![]() que puedes encontrar en el capítulo Recursos como #Curva16:
que puedes encontrar en el capítulo Recursos como #Curva16:
En primer lugar generamos las variables con los parámetros de la curva y el punto base:
| > | a:=-2: b:=50: n:=1000000000000037: base:=[29876406597393, 252423417455518]; |
| (11.11.1) |
En primer lugar, crea el alfabeto y calcula los puntos asociados a cada símbolo:
| > | Alfabeto:="ABCDEF"; |
| (11.11.2) |
| > | lista:=[]:
for i in Alfabeto do lista:=[op(lista),TextoPunto(a,b,n,i,Alfabeto,1234)]: od: lista; |
| (11.11.3) |
Seguidamente, aplica la función inversa para obtener el símbolo asociado a cada punto:
| > | A:=NULL:
for i in lista do A:=A,PuntoTexto(a,b,n,i,Alfabeto,1234): od: cat(A); |
| (11.11.4) |
Utiliza la función GeneraClaveCE de la librería CurvasElipt para crear claves de 5, 10 y 15 dígitos. Para ello utiliza la curva ![]() en
en ![]() con el punto base [29876406597393, 252423417455518] que puedes encontrar en el capítulo Recursos como #Curva16:
con el punto base [29876406597393, 252423417455518] que puedes encontrar en el capítulo Recursos como #Curva16:
En primer lugar asignamos los parámetros de la curva elíptica a variables:
| > | a:=-2: b:=50: n:=1000000000000037: base:=[29876406597393, 252423417455518]: |
Seguidamente generamos las claves de 5, 10 y 15 dígitos:
| > | clave1:=GeneraClaveCE(a,b,n,base,5,priv1); |
| (11.12.1) |
| > | priv1; |
| (11.12.2) |
| > | clave2:=GeneraClaveCE(a,b,n,base,10,priv2); |
| (11.12.3) |
| > | priv2; |
| (11.12.4) |
| > | clave3:=GeneraClaveCE(a,b,n,base,15,priv3); |
| (11.12.5) |
| > | priv3; |
| (11.12.6) |
A continuación, comprueba los resultados anteriores aplicando las fórmulas comentadas en el apartado anterior:
| > | MúltiploPunto(a,b,n,priv1[1],clave1[2]); |
| (11.12.7) |
Comprobamos que el resultado coincide:
| > | is(%=clave1[1]); |
| (11.12.8) |
Procedemos del mismo modo con los otros dos casos:
| > | MúltiploPunto(a,b,n,priv2[1],clave2[2]); |
| (11.12.9) |
| > | is(%=clave2[1]); |
| (11.12.10) |
| > | MúltiploPunto(a,b,n,priv3[1],clave3[2]); |
| (11.12.11) |
| > | is(%=clave3[1]); |
| (11.12.12) |
| > |
Supón dos usuarios, Alicia y Bob, que quieren enviarse mensajes de modo seguro. Sigue el esquema anteriormente explicado, crea un mensaje de texto y cífralo para que Bob se lo envíe a Alicia. Una vez que Bob lo haya recibido, desencriptalo para comprobar que el resultado es correcto. Se recomienda la utilización de las funciones para cifrar y descifrar CifrarCE y DescifrarCE de la librería CurvasElipt. Para ello utiliza la curva ![]() en
en ![]() con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15:
con el punto base [100098, 15890596801] que puedes encontrar en el capítulo Recursos como #Curva15:
Creamos las variables que representarán los parámetros de la curva y el punto base:
| > | a:=3101: b:=2005: n:=123456789059: base:=[100098, 15890596801]: |
En primer lugar, se generan las claves pública y privada para Alicia y Bob. Tomaremos, por ejemplo, una clave de 5 dígitos.
| > | clavePúblicaAlicia:=GeneraClaveCE(a,b,n,base,5,privadaAlicia); |
| (11.13.1) |
| > | clavePúblicaBob:=GeneraClaveCE(a,b,n,base,5,privadaBob); |
| (11.13.2) |
Sus claves privadas serán:
| > | privadaAlicia; |
| (11.13.3) |
| > | privadaBob; |
| (11.13.4) |
Bob, quiere enviar el siguiente mensaje a Alicia:
| > | mensaje:="¡Hola! ¿Qué tal? Estoy realizando una prueba del criptosistema de ElGamal."; |
| (11.13.5) |
A continuación Bob cifra el mensaje con la clave pública de Alicia (como alfabeto utilizaremos la variable castellano, contenida en la librería CurvasElipt):
| > | criptoBob:=CifrarCE(a,b,n,mensaje,castellano,clavePúblicaAlicia); |
| (11.13.6) |
Cuando Alicia lo recibe, lo desencripta con su clave privada y puede leer el mensaje en claro:
| > | DescifrarCE(a,b,n,criptoBob,castellano,privadaAlicia); |
| (11.13.7) |
Calcula una curva elíptica que tenga, al menos, 13 puntos y determina un punto base para ésta.
NOTA: Esta solución debe tomarse como referencia o guía para el cálculo. Al elegir los elementos aleatoriamente, se obtendrán resultados distintos.
En primer lugar debemos aplicar el teorema de Hasse seleccionar un cuerpo = ![]() que satisfaga la cota mínima de puntos en 13. Entonces, debemos encontrar un número p que cumpla que (p + 1) – 2
que satisfaga la cota mínima de puntos en 13. Entonces, debemos encontrar un número p que cumpla que (p + 1) – 2 ![]() ≥ N, siendo N el número de puntos de la curva elíptica, para establecer una cota inferior sobre el número de puntos.
≥ N, siendo N el número de puntos de la curva elíptica, para establecer una cota inferior sobre el número de puntos.
Calculamos el valor de p:
| > | N:=13:
evalf(solve((p+1) - 2*(p)^(1/2)>=N)); |
| (11.14.1) |
Vemos que el valor mínimo de p que cumple la condición es 21.21110255 por lo que tomamos el siguiene número, que será el 22. Por lo tanto, p ≥ 22.
Comprobamos una curva elíptica de un cuerpo = ![]() con p ≥ 22 tiene al menos 13 puntos:
con p ≥ 22 tiene al menos 13 puntos:
| > | p:=22:
cota_inferior:=evalf((p+1) - 2*(p)^(1/2)); cota_superior:=evalf((p+1) + 2*(p)^(1/2)); |
| (11.14.2) |
Por lo tanto, tendrá al menos 14 puntos y cumple la condición que buscamos para generar la curva. Por otra parte p debe ser un número primo, por lo que para fijar su valor, tomaremos el siguiente número primo a 22 (aunque se puede tomar cualquier valor primo mayor que 22):
| > | p:=nextprime(22); |
| (11.14.3) |
A continuación procedemos del siguiente modo:
1. Tomamos tres elementos cualesquiera de ![]() (para este caso concreto
(para este caso concreto ![]() ) que llamaremos x, y, a.
) que llamaremos x, y, a.
| > | x:=17; y:=17; a:=5; |
| (11.14.4) |
2. Calculamos b := ![]() – (
– (![]() + ax)
+ ax)
| > | b:= y^2 -(x^3 + a*x) mod p; |
| (11.14.5) |
3. Comprobamos que ![]() + ax + b no tiene raíces múltiples (esto es, que 4
+ ax + b no tiene raíces múltiples (esto es, que 4 ![]() + 27
+ 27![]() ≠ 0). Si esta condición no se verifica, volvemos al punto 1.
≠ 0). Si esta condición no se verifica, volvemos al punto 1.
| > | is((4*a^3 + 27*b^2) mod p <> 0); |
| (11.14.6) |
Como no se ha verificado la condición anterior, volvemos al punto1:
1. Tomamos tres elementos cualesquiera de ![]() (para este caso concreto
(para este caso concreto ![]() ) que llamaremos x, y, a.
) que llamaremos x, y, a.
| > | x:=13; y:=7; a:=16; |
| (11.14.7) |
2. Calculamos b := ![]() – (
– (![]() + ax)
+ ax)
| > | b:= y^2 -(x^3 + a*x) mod p; |
| (11.14.8) |
3. Comprobamos que ![]() + ax + b no tiene raíces múltiples (esto es, que 4
+ ax + b no tiene raíces múltiples (esto es, que 4 ![]() + 27
+ 27![]() ≠ 0). Si esta condición no se verifica, volvemos al punto 1.
≠ 0). Si esta condición no se verifica, volvemos al punto 1.
| > | is(4*a^3 + 27*b^2 mod p <> 0); |
| (11.14.9) |
4. Fijamos B := (x, y) el punto de la curva elíptica.
| > | B:=[x,y]; |
| (11.14.10) |
Por último fijamos a y b:
| > | a:=a mod p; b:=b mod p; |
| (11.14.11) |
Por lo tanto la curva será ![]() en
en ![]() y B = [13, 7] un punto de la curva.
y B = [13, 7] un punto de la curva.
Genera claves de tamaño 1 a 6 dígitos para el criptosistema de ElGamal y para el criptosistema de Curvas Elípticas. A continuación, realiza el criptoanálisis de cada una de ellas y guarda sus tiempos de ejecución para representarlos en una gráfica. Compara los resultados obtenidos. ¿Qué conclusiones obtienes?
Utilizamos la cúbica ![]() en
en ![]() con el punto base [100098, 15890596801].
con el punto base [100098, 15890596801].
| > | a:=3101: b:=2005: n:=123456789059: base:=[100098, 15890596801]: |
En primer lugar generamos las 6 claves para ElGamal:
| > | clave1EG:=GeneraClaveGamal(1,priv1EG); |
| (11.15.1) |
| > | priv1EG; |
| (11.15.2) |
| > | clave2EG:=GeneraClaveGamal(2,priv2EG); |
| (11.15.3) |
| > | priv2EG; |
| (11.15.4) |
| > | clave3EG:=GeneraClaveGamal(3,priv3EG); |
| (11.15.5) |
| > | priv3EG; |
| (11.15.6) |
| > | clave4EG:=GeneraClaveGamal(4,priv4EG); |
| (11.15.7) |
| > | priv4EG; |
| (11.15.8) |
| > | clave5EG:=GeneraClaveGamal(5,priv5EG); |
| (11.15.9) |
| > | priv5EG; |
| (11.15.10) |
| > | clave6EG:=GeneraClaveGamal(6,priv6EG); |
| (11.15.11) |
| > | priv6EG; |
| (11.15.12) |
Seguidamente procedemos a realizar sus correspondientes criptoanálisis almacenando sus tiempos:
| > | t:=time(); |
| (11.15.13) |
| > | criptoanálisis1EG:=LogaritmoDiscreto(clave1EG[2],clave1EG[1],clave1EG[3]); |
| (11.15.14) |
| > | t1EG:=time()-t; |
| (11.15.15) |
| > | is(criptoanálisis1EG = priv1EG[2]); |
| (11.15.16) |
| > | t:=time(); |
| (11.15.17) |
| > | criptoanálisis2EG:=LogaritmoDiscreto(clave2EG[2],clave2EG[1],clave2EG[3]); |
| (11.15.18) |
| > | t2EG:=time()-t; |
| (11.15.19) |
| > | is(criptoanálisis2EG = priv2EG[2]); |
| (11.15.20) |
| > | t:=time(); |
| (11.15.21) |
| > | criptoanálisis3EG:=LogaritmoDiscreto(clave3EG[2],clave3EG[1],clave3EG[3]); |
| (11.15.22) |
| > | t3EG:=time()-t; |
| (11.15.23) |
| > | is(criptoanálisis3EG = priv3EG[2]); |
| (11.15.24) |
| > | t:=time(); |
| (11.15.25) |
| > | criptoanálisis4EG:=LogaritmoDiscreto(clave4EG[2],clave4EG[1],clave4EG[3]); |
| (11.15.26) |
| > | t4EG:=time()-t; |
| (11.15.27) |
| > | is(criptoanálisis4EG = priv4EG[2]); |
| (11.15.28) |
| > | t:=time(); |
| (11.15.29) |
| > | criptoanálisis5EG:=LogaritmoDiscreto(clave5EG[2],clave5EG[1],clave5EG[3]); |
| (11.15.30) |
| > | t5EG:=time()-t; |
| (11.15.31) |
| > | is(criptoanálisis5EG = priv5EG[2]); |
| (11.15.32) |
| > | t:=time(); |
| (11.15.33) |
| > | criptoanálisis6EG:=LogaritmoDiscreto(clave6EG[2],clave6EG[1],clave6EG[3]); |
| (11.15.34) |
| > | t6EG:=time()-t; |
| (11.15.35) |
| > | is(criptoanálisis6EG = priv6EG[2]); |
| (11.15.36) |
A continuación, generamos las 6 claves para curvas elípticas:
| > | clave1CE:=GeneraClaveCE(a,b,n,base,1,priv1CE); |
| (11.15.37) |
| > | priv1CE; |
| (11.15.38) |
| > | clave2CE:=GeneraClaveCE(a,b,n,base,2,priv2CE); |
| (11.15.39) |
| > | priv2CE; |
| (11.15.40) |
| > | clave3CE:=GeneraClaveCE(a,b,n,base,3,priv3CE); |
| (11.15.41) |
| > | priv3CE; |
| (11.15.42) |
| > | clave4CE:=GeneraClaveCE(a,b,n,base,4,priv4CE); |
| (11.15.43) |
| > | priv4CE; |
| (11.15.44) |
| > | clave5CE:=GeneraClaveCE(a,b,n,base,5,priv5CE); |
| (11.15.45) |
| > | priv5CE; |
| (11.15.46) |
| > | clave6CE:=GeneraClaveCE(a,b,n,base,6,priv6CE); |
| (11.15.47) |
| > | priv6CE; |
| (11.15.48) |
Ahora aplicamos el criptoanálisis a las claves para el criptosistema de curvas elípticas:
| > | t:=time(); |
| (11.15.49) |
| > | criptoanálisis1CE:=LogaritmoPunto(a,b,n,clave1CE[2],clave1CE[1]); |
| (11.15.50) |
| > | t1CE:=time()-t; |
| (11.15.51) |
| > | is(criptoanálisis1CE = priv1CE[1]); |
| (11.15.52) |
| > | t:=time(); |
| (11.15.53) |
| > | criptoanálisis2CE:=LogaritmoPunto(a,b,n,clave2CE[2],clave2CE[1]); |
| (11.15.54) |
| > | t2CE:=time()-t; |
| (11.15.55) |
| > | is(criptoanálisis2CE = priv2CE[1]); |
| (11.15.56) |
| > | t:=time(); |
| (11.15.57) |
| > | criptoanálisis3CE:=LogaritmoPunto(a,b,n,clave3CE[2],clave3CE[1]); |
| (11.15.58) |
| > | t3CE:=time()-t; |
| (11.15.59) |
| > | is(criptoanálisis3CE = priv3CE[1]); |
| (11.15.60) |
| > | t:=time(); |
| (11.15.61) |
| > | criptoanálisis4CE:=LogaritmoPunto(a,b,n,clave4CE[2],clave4CE[1]); |
| (11.15.62) |
| > | t4CE:=time()-t; |
| (11.15.63) |
| > | is(criptoanálisis4CE = priv4CE[1]); |
| (11.15.64) |
| > | t:=time(); |
| (11.15.65) |
| > | criptoanálisis5CE:=LogaritmoPunto(a,b,n,clave5CE[2],clave5CE[1]); |
| (11.15.66) |
| > | t5CE:=time()-t; |
| (11.15.67) |
| > | is(criptoanálisis5CE = priv5CE[1]); |
| (11.15.68) |
| > | t:=time(); |
| (11.15.69) |
| > | criptoanálisis6CE:=LogaritmoPunto(a,b,n,clave6CE[2],clave6CE[1]); |
| (11.15.70) |
| > | t6CE:=time()-t; |
| (11.15.71) |
| > | is(criptoanálisis6CE = priv6CE[1]); |
| (11.15.72) |
Por último, pintamos una gráfica con los tiempos de ambos criptoanálisis para poder comparar los resultados:
| > | with(plots): |
| > | tEG:=plot({[1,t1EG],[2,t2EG],[3,t3EG],[4,t4EG],[5,t5EG],[6,t6EG]},dígitos=0..6,tiempo,color=red): |
| > | tCE:=plot({[[1,t1CE],[2,t2CE],[3,t3CE],[4,t4CE],[5,t5CE],[6,t6CE]]},dígitos=0..6,tiempo,color=green): |
| > | plots[display](tEG); |
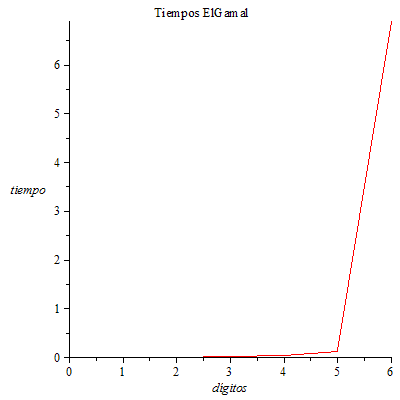 |
| > | plots[display](tCE); |
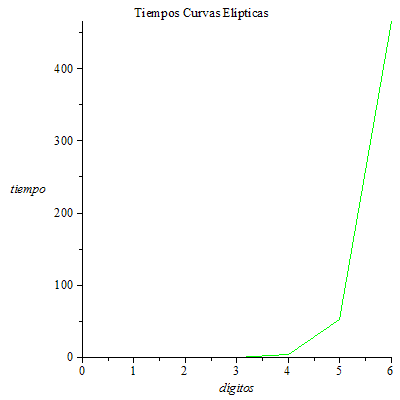 |
| > | plots[display](tEG,tCE); |
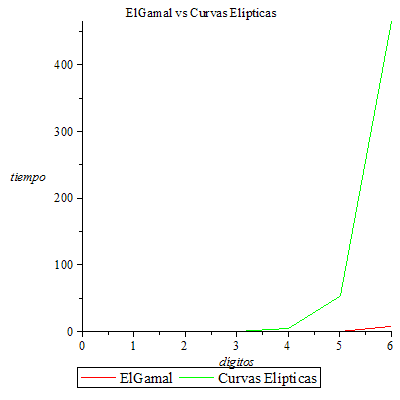 |
Conclusiones: Si comparamos los tiempos para los criptoanálisis de las claves con el mismo tamaño, comprobamos que los tiempos para romper una clave del criptosistema de curvas elípticas son mayores que para romper los del criptosistema de ElGamal. Esto significa que para tamaños de clave menores se obtiene un mayor nivel de seguridad con el criptosistema de curvas elípticas.
Conceptos
Algoritmo de Exponenciación Modular Rápida (AEMR)
Con este algoritmo se pueden calcular potencias en aritmética modular de un modo eficiente. La idea es hacer cuadrados sucesivos, basándose en la expresión del exponente en base 2.
La descripción del algoritmo es la siguiente:
Dados a ∈ ℤ*, e ∈ ℕ para calcular ![]() se procede del siguiente modo:
se procede del siguiente modo:
1) Si e = 0, devolver 1
2) Definir q := e, p := 1 y c := a (mod n)
3) Mientras q ≠ 1, repetir:
a) Dividir q entre 2 generando el cociente q y el resto rb) Si r = 1 entonces actualizar p := p • c (mod n)c) Calcular c := ![]() (mod n)
(mod n)
4) Devolver p • c (mod n)
Ejemplos
Vamos a realizar el cálculo de ![]() mod 9 con el algoritmo de exponenciación modular rápida:
mod 9 con el algoritmo de exponenciación modular rápida:
Para ello seguimos el paso 1 y como e ≠ 0, pasamos al paso 2:
| > | q:=10; p:=1; c:= 5 mod 9; |
| (12.1.2.1) |
Entramos en el bucle del paso 3 y generamos el cociente q y el resto r mientras q ≠ 1:
| > | r:=irem(q,2); q:=iquo(q,2); |
| (12.1.2.2) |
Si r = 1 actualizamos p:
| > | if r = 1 then p:=p*c mod 9;
else p:=p; end if; |
| (12.1.2.3) |
Calculamos ![]() mod 9:
mod 9:
| > | c:=c&^2 mod 9; |
| (12.1.2.4) |
Repetimos la secuencia hasta que q = 1:
| > | r:=irem(q,2);
if q <> 1 then q:=iquo(q,2); else resultado:=p*c mod 9; end if; |
| (12.1.2.5) |
| > | if r = 1 then p:=p*c mod 9;
else p:=p; end if; |
| (12.1.2.6) |
| > | c:=c&^2 mod 9; |
| (12.1.2.7) |
| > | r:=irem(q,2);
if q <> 1 then q:=iquo(q,2); else resultado:=p*c mod 9; end if; |
| (12.1.2.8) |
| > | if r = 1 then p:=p*c mod 9;
else p:=p; end if; |
| (12.1.2.9) |
| > | c:=c&^2 mod 9; |
| (12.1.2.10) |
| > | r:=irem(q,2);
if q <> 1 then q:=iquo(q,2); else resultado:=p*c mod 9; end if; |
| (12.1.2.11) |
Comprobación del resultado:
| > | 5&^10 mod 9; |
| (12.1.2.12) |
Una tabla resumiendo lo anterior quedaría del siguiente modo (i = nº de iteración; q = cociente; r = resto; p = producto; c = potencias de 2):
i |
q |
r |
p |
c |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|||||||||||||||||||||||
Dos números enteros son congruentes módulo n si al dividirlos entre n obtenemos el mismo resto. Cuando a es congruente con b módulo n se escribe a ≡ b (mod n). La relación de congruencia es una relación de equivalencia y, si el módulo es n, hay n clases de equivalencia correspondientes a los diferentes restos de dividir por n.
La aritmética modular es un sistema aritmético para clases de equivalencia de números enteros llamadas clases de congruencia. Las operaciones son la suma y el producto módulo n en el conjunto ℤn = {0, …, n – 1}.
Si p es un número primo, el conjunto ℤp, con las operaciones de suma y producto, es un cuerpo. Por tanto para todo c ≠ 0 existe un elemento inverso ![]() , tal que
, tal que ![]() ·c ≡1 (mod p). Esto no ocurre en ℤn cuando n no es primo. Por ejemplo, 2 no tiene inverso en ℤ6.
·c ≡1 (mod p). Esto no ocurre en ℤn cuando n no es primo. Por ejemplo, 2 no tiene inverso en ℤ6.
Ejemplos
Vamos a comprobar que 2 no tiene inverso en ℤ6:
| > | for i to 6-1 do i*2 mod 6 end do; |
| (12.2.2.1) |
Como podemos ver, no hay ningún elemento en ℤ6 que cumpla la condición ![]() ·c ≡1 (mod p) para c = 2.
·c ≡1 (mod p) para c = 2.
Ahora vamos a calcular las clases de equivalencia para ![]() :
:
| > | Z[7]:={0 mod 7, 1 mod 7, 2 mod 7, 3 mod 7, 4 mod 7, 5 mod 7, 6 mod 7}; |
| (12.2.2.2) |
Veamos cuál es la relación de congruencia del 152 en ![]() :
:
| > | 152 mod 7; |
| (12.2.2.3) |
Clases de equivalencia para ![]() :
:
| > | Z[5]:={0 mod 5, 1 mod 5, 2 mod 5, 3 mod 5, 4 mod 5}; |
| (12.2.2.4) |
Equivalente numérico de un mensaje
Para poder aplicar procedimientos matemáticos de cifrado a un mensaje de texto es necesario convertirlo en un número o secuencia de números. Esto se puede hacer símbolo a símbolo, asignando a cada símbolo un número, por ejemplo su posición en el alfabeto que se esté usando, o bien asignando un número a una cadena de símbolos. En este caso, el valor numérico del mensaje m := m1m2…ml sobre un alfabeto ordenado de tamaño r es:
m1 ![]() + m2
+ m2 ![]() + ⋯ + m l-1 r + ml
+ ⋯ + m l-1 r + ml
donde los símbolos m1, m2, …, ml se identifican con sus posiciones dentro del alfabeto.
Ejemplos
Creamos dos alfabetos para las pruebas:
| > | alfabeto1:="ABCO"; |
| (12.3.2.1) |
| > | r1:=length(alfabeto1); |
| (12.3.2.2) |
| > | alfabeto2:="OACB"; |
| (12.3.2.3) |
| > | r2:=length(alfabeto2); |
| (12.3.2.4) |
Hallamos el valor numérico de las palabras OCA y ABACO para ambos alfabetos aplicando m1 ![]() + m2
+ m2 ![]() + ⋯ + m l-1 r + ml :
+ ⋯ + m l-1 r + ml :
Para el alfabeto1:
| > | OCA:=SearchText("O",alfabeto1)*r1^2 + SearchText("C",alfabeto1)*r1^1 + SearchText("A",alfabeto1)*r1^0; |
| (12.3.2.5) |
| > | ABACO:=SearchText("A",alfabeto1)*r1^4 + SearchText("B",alfabeto1)*r1^3 + SearchText("A",alfabeto1)*r1^2 + SearchText("C",alfabeto1)*r1^1 + SearchText("O",alfabeto1)*r1^0; |
| (12.3.2.6) |
Para el alfabeto2:
| > | OCA:=SearchText("O",alfabeto2)*r1^2 + SearchText("C",alfabeto2)*r1^1 + SearchText("A",alfabeto2)*r1^0; |
| (12.3.2.7) |
| > | ABACO:=SearchText("A",alfabeto2)*r1^4 + SearchText("B",alfabeto2)*r1^3 + SearchText("A",alfabeto2)*r1^2 + SearchText("C",alfabeto2)*r1^1 + SearchText("O",alfabeto2)*r1^0; |
| (12.3.2.8) |
Este proceso se puede realizar con la función MensajeNumérico de la librería CurvasElipt y se puede recuperar el mensaje original mediante la función MensajeTexto.
Logaritmo Discreto para Números Enteros
Sea g una raíz primitiva de n. Si ![]() = 1, llamamos Logarirmo Discreto de a en la base g módulo n al menor entero no negativo k tal que a ≡
= 1, llamamos Logarirmo Discreto de a en la base g módulo n al menor entero no negativo k tal que a ≡ ![]() (mod n). Lo denotamos
(mod n). Lo denotamos ![]() (mod n).
(mod n).
![]() :
: ![]() → {1, ..., φ(n)} donde
→ {1, ..., φ(n)} donde ![]() = {
= {![]() = 1}
= 1}
a → ![]() = k si
= k si ![]() ≡ a (mod n)
≡ a (mod n)
El cálculo del logaritmo discreto es un problema intratable, pues por el momento no se conocen algoritmos eficientes que lo resuelvan. De ahí (como el problema de la factorización) su aplicación en criptología.
La función LogaritmoDiscreto de la librería CurvasElipt obtiene el valor del logaritmo discreto por exploración.
Ejemplos
Tabla del logaritmo discreto en ![]() con base 3. Se denota
con base 3. Se denota ![]() (mod 7):
(mod 7):
| > | for a to 7-1 do ('log[3]')(a) = LogaritmoDiscreto(3, 7, a) end do; |
| (12.4.2.1) |
Para comprobar que lo anterior es correcto realizamos la operación ![]() (mod 7):
(mod 7):
| > | for a to 7-1 do 3&^LogaritmoDiscreto(3, 7, a) mod 7 end do; |
| (12.4.2.2) |
De este modo comprobamos que ![]() (mod 7) = x ⇔
(mod 7) = x ⇔ ![]() ≡ a (mod 7)
≡ a (mod 7)
Dado n ∈ ℕ, n > 1 y un entero, a, con mcd (a,n) = 1, llamamos orden de a módulo n, y lo notamos ordn (a), al menor entero positivo r tal que ![]() ≡ 1 (mod n).
≡ 1 (mod n).
Ejemplos
Vamos a calcular los órdenes de los elementos de ![]() . Para ello tiene que cumplirse que
. Para ello tiene que cumplirse que ![]() ≡ 1 (mod n).
≡ 1 (mod n).
| > | 1&^1 mod 7; |
| (12.5.2.1) |
Por lo que ord7 (1) = 1.
| > | 2&^1 mod 7; |
| (12.5.2.2) |
| > | 2&^2 mod 7; |
| (12.5.2.3) |
| > | 2&^3 mod 7; |
| (12.5.2.4) |
Por lo que ord7 (2) = 3.
| > | 3&^1 mod 7; |
| (12.5.2.5) |
| > | 3&^2 mod 7; |
| (12.5.2.6) |
| > | 3&^3 mod 7; |
| (12.5.2.7) |
| > | 3&^4 mod 7; |
| (12.5.2.8) |
| > | 3&^5 mod 7; |
| (12.5.2.9) |
| > | 3&^6 mod 7; |
| (12.5.2.10) |
Por lo que ord7 (3) = 6.
| > | 4&^1 mod 7; |
| (12.5.2.11) |
| > | 4&^2 mod 7; |
| (12.5.2.12) |
| > | 4&^3 mod 7; |
| (12.5.2.13) |
Por lo que ord7 (4) = 3.
| > | 5&^1 mod 7; |
| (12.5.2.14) |
| > | 5&^2 mod 7; |
| (12.5.2.15) |
| > | 5&^3 mod 7; |
| (12.5.2.16) |
| > | 5&^4 mod 7; |
| (12.5.2.17) |
| > | 5&^5 mod 7; |
| (12.5.2.18) |
| > | 5&^6 mod 7; |
| (12.5.2.19) |
Por lo que ord7 (5) = 6.
| > | 6&^1 mod 7; |
| (12.5.2.20) |
| > | 6&^2 mod 7; |
| (12.5.2.21) |
Por lo que ord7 (6) = 2.
Se trata de la función:
φ: ℕ* → ℕ
n → φ(n) = card(ℤn*) = card({a ∈ ℤ | 0 ≤ a < n y mcd(a, n) = 1 })
El valor de φ(n) puede verse como el número de:
(a) Unidades (elementos con inverso) de ℤn(b) Enteros positivos y menores que n que son primos con n(c) Enteros positivos y menores que n que tienen inverso módulo n
Entre sus propiedades cabe destacar:
φ(1) = 1
Si p ∈ ℕ* es primo, φ(p) = p – 1
Si p ∈ ℕ* es primo, entonces φ(![]() ) =
) = ![]() –
– ![]() =
= ![]() (1 –
(1 – ![]() )
)
Si n, m ∈ ℕ* y mcd (m, n) = 1, entonces φ(n•m) = φ(n) • φ(m)
Teorema de Euler: Si n ∈ ℕ* es primo con a, entonces ![]() ≡ 1 (mod n)
≡ 1 (mod n)
La función de Maple numtheory[phi] calcula el valor φ(n) para el valor entero n que se le pase como parámetro.
Ejemplos
Vamos a calcular φ(2):
| > | numtheory[phi](2); |
| (12.6.2.1) |
Comprobamos el resultado según las propiedades anteriores. Por la propiedad 1 tenemos lo siguiente:
| > | 2-1; |
| (12.6.2.2) |
Como vemos, coinciden los resultados.
Ahora vamos a calcular φ(9):
| > | numtheory[phi](9); |
| (12.6.2.3) |
Comprobamos el resultado según las propiedades anteriores. Por la propiedad 3 tenemos que φ(9) = φ(![]() ), entonces:
), entonces:
| > | 3^2 * (1 - 1/3); |
| (12.6.2.4) |
Como vemos, coinciden los resultados.
Por último, vamos a calcular φ(36):
| > | numtheory[phi](36); |
| (12.6.2.5) |
Comprobamos el resultado según las propiedades anteriores. Tenemos que φ(36) = φ(![]() ) y aplicando la propiedad 4 φ(
) y aplicando la propiedad 4 φ(![]() ) = φ(
) = φ(![]() ) · φ(
) · φ(![]() ) = entonces:
) = entonces:
| > | (2^2*(1-1/2))*(3^2*(1-1/3)); |
| (12.6.2.6) |
Como vemos, coinciden los resultados.
Una raíz primitiva módulo n es un generador del grupo ![]() .
.
Si ordn (a) =
φ(n)
, entonces a̅ es un generador de ![]() , o también se dice que a es una raíz primitiva módulo n.
, o también se dice que a es una raíz primitiva módulo n.
Para determinar la existencia de raíces primitivas es útil la siguiente propiedad:
Proposición
Si en ℤn* hay un generador, entonces hay φ(φ(n)) generadores. Además:
Sea n ∈ ℕ, n > 1: n tiene raíz primitiva si y sólo si:n = 2, 4, ![]() ó 2
ó 2![]() , siendo p primo impar, α ∈ ℕ*
, siendo p primo impar, α ∈ ℕ*
Si p es primo, entonces en ℤp hay φ(p – 1) raíces primitivas.
Ejemplos
Vamos a calcular los órdenes de los elementos de ![]() indicando cuáles de ellos son generadores. Para ello se tiene que cumplir que ordn (a) =
φ(n)
.
indicando cuáles de ellos son generadores. Para ello se tiene que cumplir que ordn (a) =
φ(n)
.
Calculamos φ(7):
| > | phi:=numtheory[phi](7); |
| (12.7.2.1) |
A continuacuón calculamos ordn (a):
| > | 1&^1 mod 7; |
| (12.7.2.2) |
Por lo que ord7 (1) = 1. Como ord7 (1) ≠ φ(7), no es raíz primitiva. Hay elementos de ![]() que no se pueden poner como potencia de 1.
que no se pueden poner como potencia de 1.
| > | 2&^1 mod 7; |
| (12.7.2.3) |
| > | 2&^2 mod 7; |
| (12.7.2.4) |
| > | 2&^3 mod 7; |
| (12.7.2.5) |
Por lo que ord7 (2) = 3. Como ord7 (2) ≠ φ(7), no es raíz primitiva. Hay elementos de ![]() que no se pueden poner como potencia de 2.
que no se pueden poner como potencia de 2.
| > | 3&^1 mod 7; |
| (12.7.2.6) |
| > | 3&^2 mod 7; |
| (12.7.2.7) |
| > | 3&^3 mod 7; |
| (12.7.2.8) |
| > | 3&^4 mod 7; |
| (12.7.2.9) |
| > | 3&^5 mod 7; |
| (12.7.2.10) |
| > | 3&^6 mod 7; |
| (12.7.2.11) |
Por lo que ord7 (3) = 6. Como ord7 (3) = φ(7), 3 es una raíz primitiva mod 7 o generador de ![]() . Todo elemento de
. Todo elemento de ![]() se puede poner como potencia de 3.
se puede poner como potencia de 3.
| > | 4&^1 mod 7; |
| (12.7.2.12) |
| > | 4&^2 mod 7; |
| (12.7.2.13) |
| > | 4&^3 mod 7; |
| (12.7.2.14) |
Por lo que ord7 (4) = 3. Como ord7 (4) ≠ φ(7), no es raíz primitiva. Hay elementos de ![]() que no se pueden poner como potencia de 4.
que no se pueden poner como potencia de 4.
| > | 5&^1 mod 7; |
| (12.7.2.15) |
| > | 5&^2 mod 7; |
| (12.7.2.16) |
| > | 5&^3 mod 7; |
| (12.7.2.17) |
| > | 5&^4 mod 7; |
| (12.7.2.18) |
| > | 5&^5 mod 7; |
| (12.7.2.19) |
| > | 5&^6 mod 7; |
| (12.7.2.20) |
Por lo que ord7 (5) = 6. Como ord7 (5) = φ(7), 5 es una raíz primitiva mod 7 o generador de ![]() . Todo elemento de
. Todo elemento de ![]() se puede poner como potencia de 5.
se puede poner como potencia de 5.
| > | 6&^1 mod 7; |
| (12.7.2.21) |
| > | 6&^2 mod 7; |
| (12.7.2.22) |
Por lo que ord7 (6) = 2. Como ord7 (6) ≠ φ(7), no es raíz primitiva. Hay elementos de ![]() que no se pueden poner como potencia de 6.
que no se pueden poner como potencia de 6.
Recomendaciones técnicas
¿Cómo quitar la advertencia de seguridad de grupos autoejecutables?
Al abrir nuevas pestañas con contenido autoejecutable aparecerá una advertencia como la siguiente:
Para el normal desarrollo de este curso, recomendamos pulsar la opción "Sí". De este modo podremos utilizar las funciones que contiene el curso, las páginas de ayuda, etc. Esta advertencia aparecerá cada vez que abramos una hoja de trabajo nueva con código autoejecutable ya que es la opción por defecto.
Si queremos que nuestra decisión se mantenga permanentemente, debemos ir al menú Herramientas >> Opciones...:
Se abrirá una ventana como la siguiente, en la que debemos seleccionar la pestaña "Seguridad":
Tal y como hemos comentado anteriormente la opción por defecto para "Autoejecute nivel de Seguridad" es "Avisar una vez por cada hoja de trabajo". De este modo, cada vez que abramos una hoja de trabajo con código autoejecutable aparecerá la advertencia de seguridad. Para evitar que aparezca abrimos el desplegable y seleccionamos la opción "No advertir antes de la autoejecución":
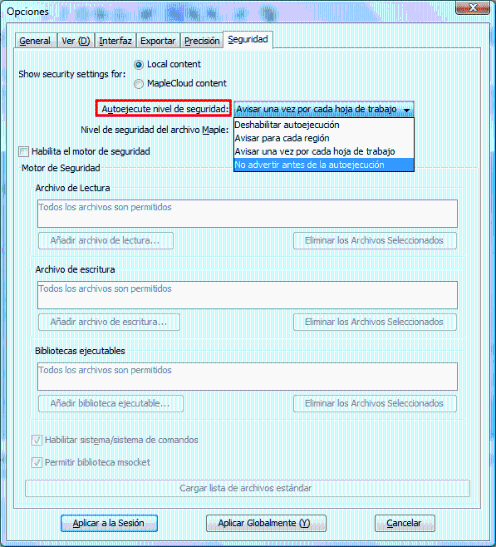
Otras opciones disponibles son:
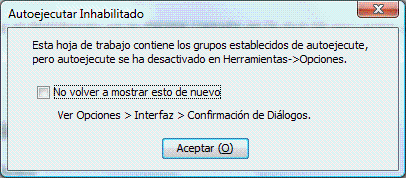
Por último y para mantener los cambios cada vez que accedamos a Maple, debemos salir del cuadro de diálogo pulsando el botón "Aplicar globalmente":
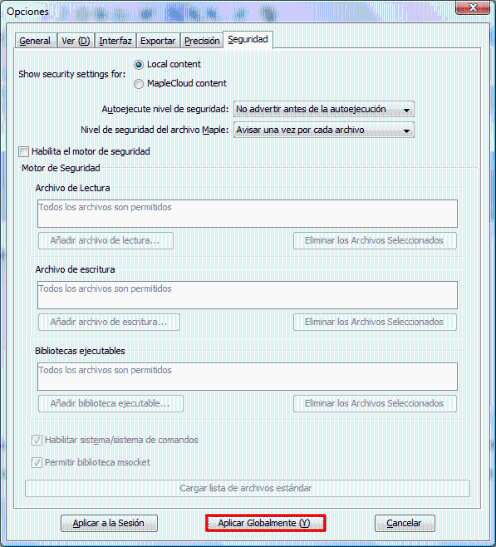
¿Cómo abrir los documentos en una pestaña nueva por defecto?
Si no hemos modificado la confirguración de Maple, cada vez que hagamos clic sobre un enlace que nos redirija a una hoja de trabajo Maple, aparecerá una ventana como la siguiente:
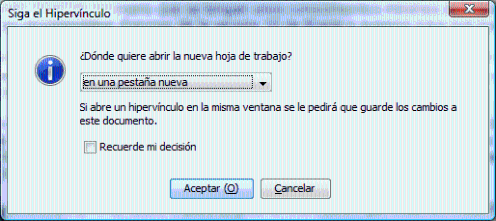
Si abrimos el desplegable, tendremos tres opciones:
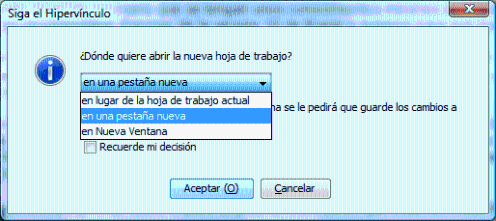
Para evitar que aparezca este mensaje cada vez que hagamos clic en un hiperenlace que nos lleva a una hoja de trabajo Maple, es suficiente con que marquemos la casilla "Recuerde mi decisión":
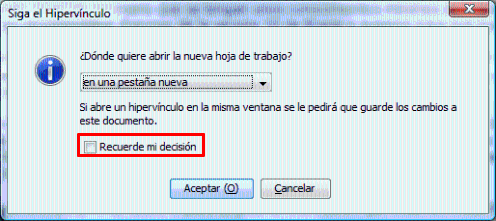
Siguiendo este procedimiento se recordará la decisión tomada durante la sesión. Sin embargo para recordarlo siempre, podemos ir al menú Herramientas >> Opciones...:
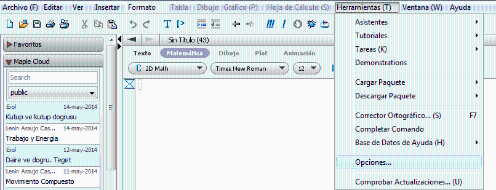
Se abrirá una ventana como la siguiente, en la que debemos seleccionar la pestaña "Interfaz":
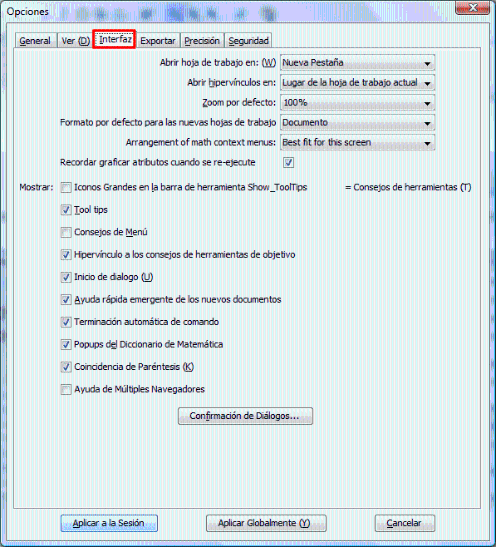
Abrimos el desplegable de "Abrir hipervínculos en:" y seleccionamos la opción de "Nueva Pestaña":
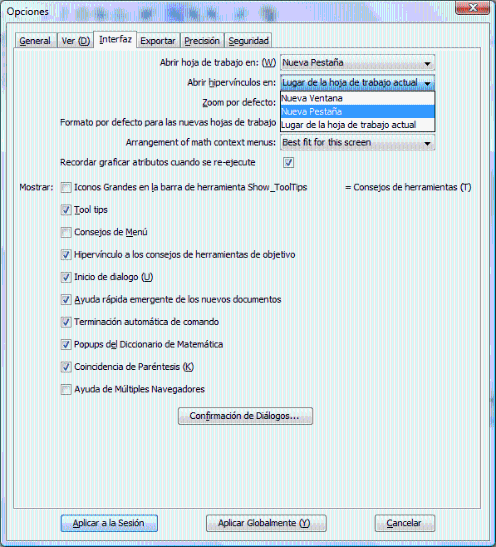
Por último y para que Maple recuerde siempre nuestra elección, debemos salir pulsando el botón "Aplicar Globalmente":
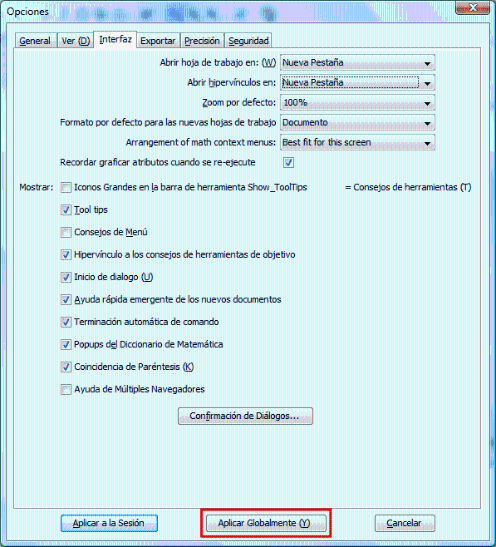
Páginas de ayuda de la librería CurvasElipt
Overview of the CurvasElipt Package
CurvasElipt[command](arguments)
command(arguments)
| > | CurvasElipt[CifrarCE](...); |
| > | with(CurvasElipt): |
| > | CifrarCE(...); |
Variable
List of CurvasElipt Package Commands
CurvasElipt[castellano] - Spanish alphabet
castellano
The first example shows how to see the elements contained in the castellano variable using the long form :
| > | restart:
libname:=libname,".": CurvasElipt[castellano]; |
| (14.2.3.1) |
Now the alphabet is shown using the short form:
| > | with(CurvasElipt):
castellano; |
| (14.2.3.2) |
The next example checks that the length of the castellano variable is 113:
| > | length(castellano); |
| (14.2.3.3) |
You can also use a character from the variable:
| > | castellano[1]; |
| (14.2.3.4) |
| > | castellano[13]; |
| (14.2.3.5) |
| > | castellano[113]; |
| (14.2.3.6) |
You can use assigment operations with this variable:
| > | A:=castellano:
A; |
| (14.2.3.7) |
| > | A[1]; |
| (14.2.3.8) |
| > | A[13]; |
| (14.2.3.9) |
| > | A[113]; |
| (14.2.3.10) |
CurvasElipt[MensajeNumérico] - Numerical equivalent of a string
CurvasElipt[MensajeTexto] - String associated to a number
MensajeNumérico(m, A)
MensajeTexto(n, A)
Parameters
m, A |
- |
strings |
n |
- |
positive integer |
"ABC" = 1 · 262 + 2 · 26 + 3 = 731
| > | libname:= libname,".": with(CurvasElipt): |
This is the process to compute the numerical equivalent:
| > | MensajeNumérico("ABC","ABC"); |
| (14.3.4.1) |
| > | 1*3^2+2*3+3; |
| (14.3.4.2) |
This is how the functions work with an only character:
| > | MensajeNumérico("B",castellano); |
| (14.3.4.3) |
| > | MensajeTexto(%,castellano); |
| (14.3.4.4) |
| > | SearchText("B",castellano); |
| (14.3.4.5) |
| > | castellano[%]; |
| (14.3.4.6) |
Next examples show the use of MensajeNumérico and MensajeTexto:
| > | MensajeNumérico("PATATA",castellano); |
| (14.3.4.7) |
| > | MensajeTexto(%,castellano); |
| (14.3.4.8) |
| > | MensajeNumérico("¡Poderoso caballero es Don Dinero! Francisco de Quevedo.",castellano); |
| (14.3.4.9) |
| > | MensajeTexto(%,castellano); |
| (14.3.4.10) |
| > | MensajeNumérico("El veloz murciélago hindú comía feliz cardillo y kiwi. La cigüeña tocaba el saxofón detrás del palenque de paja. Pangrama",castellano); |
| (14.3.4.11) |
| > | MensajeTexto(%,castellano); |
| (14.3.4.12) |
When you use a symbol that does not belong to the alphabet, it returns an error message:
| > | MensajeNumérico("«HOLA»",castellano); |
| Error, (in MensajeNumérico) El elemento '«' no pertenece al alfabeto |
CurvasElipt[GeneraClaveGamal] - Key for ElGamal Cryptosystem
GeneraClaveGamal(n, 'priv')
Parameters
n |
- |
positive integer |
priv |
- |
evaln (can be evaluated to a name) |
| > | libname:= libname,".": with(CurvasElipt): |
These examples show a warning message because their length is not safe enough:
| > | GeneraClaveGamal(1,priv1); |
| (14.4.4.1) |
| > | priv1; |
| (14.4.4.2) |
| > | GeneraClaveGamal(2,priv2); |
| (14.4.4.3) |
| > | priv2; |
| (14.4.4.4) |
If the lenght of the key is greater than or equal to 3, it will be considered safe:
| > | GeneraClaveGamal(3,priv3); |
| (14.4.4.5) |
| > | priv3; |
| (14.4.4.6) |
| > | GeneraClaveGamal(5,priv5); |
| (14.4.4.7) |
| > | priv5; |
| (14.4.4.8) |
| > | GeneraClaveGamal(8,priv8); |
| (14.4.4.9) |
| > | priv8; |
| (14.4.4.10) |
| > | clave10:=GeneraClaveGamal(10,priv10); |
| (14.4.4.11) |
| > | priv10; |
| (14.4.4.12) |
That is the β = α a mod p comprobation for "clave10" example:
| > | beta:= 2&^8415955883 mod 8697471851; |
| (14.4.4.13) |
| > | is(beta=clave10[3]); |
| (14.4.4.14) |
CurvasElipt[ElGamal] - ElGamal Cryptosystem
ElGamal(m, A, clave)
Parameters
m |
- |
string or list of positive integer lists |
A |
- |
string |
clave |
- |
positive integer list |
| > | restart;
libname:=libname,".": with(CurvasElipt): |
Keys generation: Alicia (an user) creates her keys in order to send an receive messages:
| > | clavePúblicaA:=GeneraClaveGamal(10,privA); |
| (14.5.4.1) |
Alicia's private key will be:
| > | privA; |
| (14.5.4.2) |
Then Bob (another user) creates his keys with the same goal:
| > | clavePúblicaB:=GeneraClaveGamal(10,privB); |
| (14.5.4.3) |
Bob's private key will be:
| > | privB; |
| (14.5.4.4) |
Then, Bob wants to send the next message (plaintext) to Alicia:
| > | mensaje:="¡Hola! ¿Qué tal? Estoy realizando una prueba del criptosistema de ElGamal."; |
| (14.5.4.5) |
So Bob has to encrypt the message (cryptogram) with Alicia's public key and send it to her:
| > | criptoB:=ElGamal(mensaje,castellano,clavePúblicaA); |
| (14.5.4.6) |
When Alicia receives the encrypted message, she has to decrypt it with her private key:
| > | ElGamal(criptoB,castellano,privA); |
| (14.5.4.7) |
| > | is(%=mensaje); |
| (14.5.4.8) |
We are going to answer: Alicia sends the next plaintext to Bob:
| > | mensaje2:="Este es un mensaje en respuesta a Bob. Podrá leerlo cuando lo desencripte con su clave privada ;-)"; |
| (14.5.4.9) |
Then, Alicia encrypts her message with Bob's public key and sends the cryptogram to him:
| > | criptoA:=ElGamal(mensaje2,castellano,clavePúblicaB); |
| (14.5.4.10) |
When Bob receives the cryptogram, he has to decrypt it with his private key in order to get the plaintext:
| > | ElGamal(criptoA,castellano,privB); |
| (14.5.4.11) |
| > | is(%=mensaje2); |
| (14.5.4.12) |
CurvasElipt[LogaritmoDiscreto] - Discrete logarithm
LogaritmoDiscreto(b, p, a)
Parameters
b, p, a |
- |
positive integers |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
log2 (7) (mod 9):
| > | LogaritmoDiscreto(2,9,7); |
| (14.6.4.1) |
Discrete logarithm in ℤ*7 with base = 3.
| > | for j from 1 to 7-1 do
'log[3]'(j)=LogaritmoDiscreto(3,7,j); od; |
| (14.6.4.2) |
Discrete logarithm in ℤ*7 with base = 5.
| > | for j from 1 to 7-1 do
'log[5]'(j)=LogaritmoDiscreto(5,7,j); od; |
| (14.6.4.3) |
Discrete logarithm in ℤ*19 with base = 3.
| > | for j from 1 to 19-1 do
'log[3]'(j)=LogaritmoDiscreto(3,19,j); od; |
| (14.6.4.4) |
The next error happens when the base is not a primitive rood mod p:
| > | LogaritmoDiscreto(10,33,15); |
| Error, (in LogaritmoDiscreto) La base, b = 10, no es una raíz primitiva módulo 33 |
When the number a and the n in Zn are not prime between them, the function returns an error message:
| > | LogaritmoDiscreto(2,9,3); |
| Error, (in LogaritmoDiscreto) 3 y 9 no son primos entre si |
CurvasElipt[ListarPuntos] - Points of an Elliptic Curve
ListarPuntos(a, b, n, gráfica)
ListarPuntos(a, b, n)
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
gráfica |
- |
(optional) boolean |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
The function will return the list of the points of the elliptic curve when gráfica parameter is FALSE or it is not used:
| > | ListarPuntos(-1,3,5); |
| (14.7.4.1) |
| > | ListarPuntos(1,-2,5); |
| (14.7.4.2) |
| > | ListarPuntos(0,-2,7); |
| (14.7.4.3) |
| > | ListarPuntos(0,-2,7,false); |
| (14.7.4.4) |
The next examples show the use of the parameter grafica when it is TRUE and the chart is returned as a collateral effect:
| > | ListarPuntos(-4,2,11,true); |
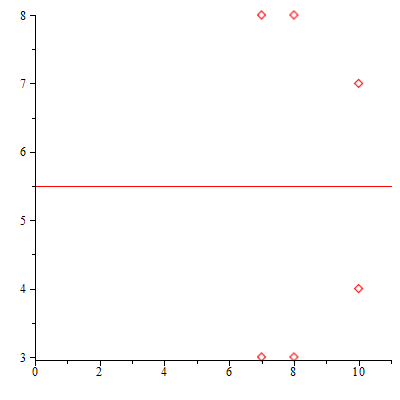 |
|
| (14.7.4.5) |
| > | ListarPuntos(1,3,11,true); |
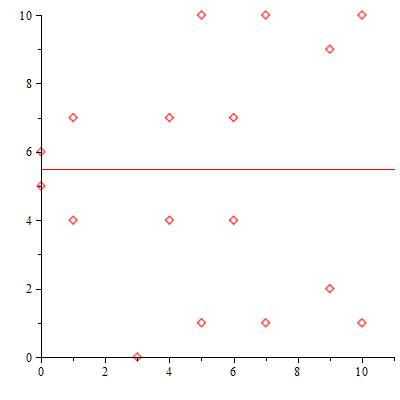 |
|
| (14.7.4.6) |
| > | ListarPuntos(1,-2,23,true); |
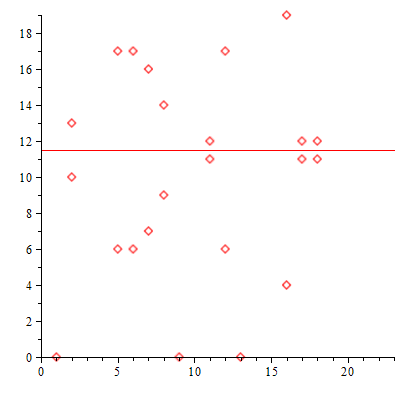 |
|
| (14.7.4.7) |
This example is an elliptic curve with a large number of points, so we only show the number of elements of the list:
| > | ListarPuntos(-2,50,14831):
nops(%); |
| (14.7.4.8) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | ListarPuntos(3,1,2); |
| Error, (in ListarPuntos) El 'n' introducido debe ser distinto de 2 y de 3 |
| > | ListarPuntos(5,1,3); |
| Error, (in ListarPuntos) El 'n' introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | ListarPuntos(3,1,4); |
| Error, (in ListarPuntos) El argumento 'n' debe ser un número primo. Se ha recibido 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | ListarPuntos(3,1,5); |
| Error, (in ListarPuntos) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
CurvasElipt[SumaPuntos] - Sum of two points of an Elliptic Curve
SumaPuntos(a, b, n, P, Q, grafica)
SumaPuntos(a, b, n, P, Q)
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
P, Q |
- |
list of two integers or infinity |
grafica |
- |
(optional) boolean |
y3 = m(x1 - x3) - y1
where m = 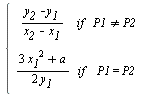
- If m = ∞ then P1 + P2 := θE
- ∀ P ∈ E: P + θE := P
| > | restart;
libname:= libname,".": with(CurvasElipt): |
If the result is infinity, it is not possible to draw a plot. So a warning message is shown with the result:
| > | SumaPuntos(1,-2,5,[1,0],[1,0],true); |
| (14.8.4.1) |
You can either avoid use the last parameter or use FALSE if you do not want a plot showing the result. Then it will be returned the result of the sum:
| > | SumaPuntos(1,-2,5,[1,0],[1,0]); |
| (14.8.4.2) |
| > | SumaPuntos(1,-2,5,[1,0],[1,0],false); |
| (14.8.4.3) |
| > | SumaPuntos(1,-2,5,[1,0],[4,1]); |
| (14.8.4.4) |
| > | SumaPuntos(1,-2,5,[1,0],[4,1],false); |
| (14.8.4.5) |
| > | SumaPuntos(1,-2,5,[1,0],[4,1],true); |
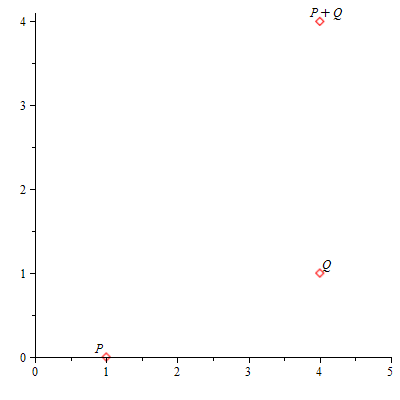 |
|
| (14.8.4.6) |
| > | SumaPuntos(1,-2,5,[4,1],[4,1],true); |
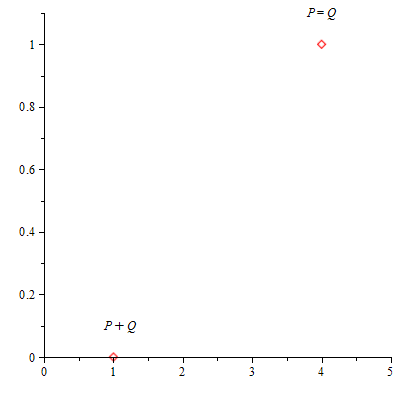 |
|
| (14.8.4.7) |
| > | SumaPuntos(1,-2,5,[4,1],[4,1],true); |
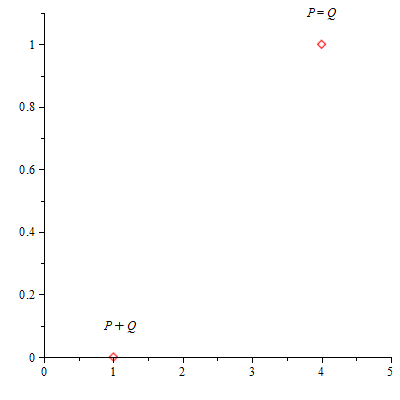 |
|
| (14.8.4.8) |
| > | SumaPuntos(-4,2,7,[0,3],[5,4],true); |
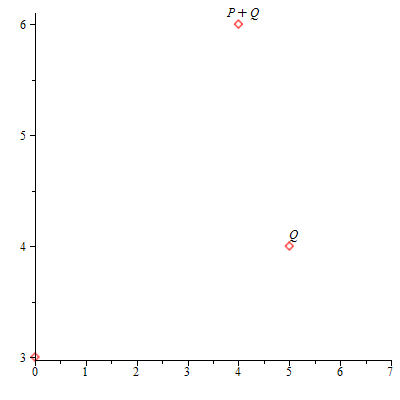 |
|
| (14.8.4.9) |
| > | SumaPuntos(-4,2,7,[4,6],[2,4],true); |
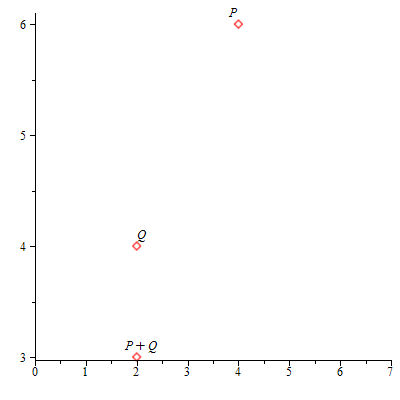 |
|
| (14.8.4.10) |
| > | SumaPuntos(-4,2,7,[2,3],[5,4],true); |
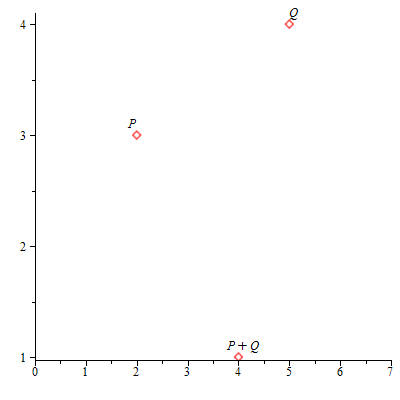 |
|
| (14.8.4.11) |
| > | SumaPuntos(-4,2,11,[7,3],[7,3],true); |
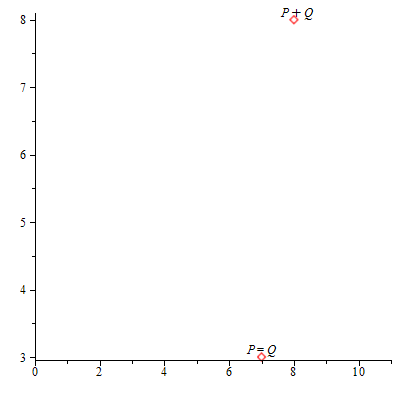 |
|
| (14.8.4.12) |
| > | SumaPuntos(-4,2,11,[10,7],[7,8],true); |
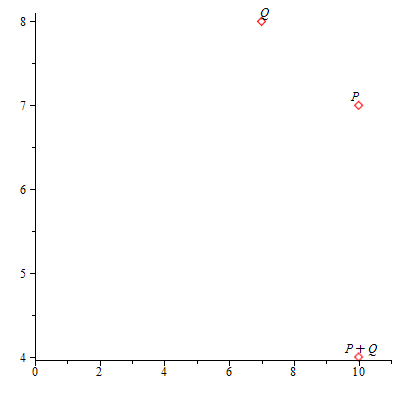 |
|
| (14.8.4.13) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | SumaPuntos(3,1,2,[0,1],[1,0]); |
| Error, (in SumaPuntos) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | SumaPuntos(5,1,3,[0,1],[1,0]); |
| Error, (in SumaPuntos) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | SumaPuntos(3,1,4,[0,1],[1,0]); |
| Error, (in SumaPuntos) El argumento 'n' debe ser un número primo. Se ha recibido 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | SumaPuntos(3,1,5,[0,1],[1,0]); |
| Error, (in SumaPuntos) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
When the points do not belong to the elliptic curve, the function returns an error message:
| > | SumaPuntos(1,-2,5,[2,0],[1,0],true); |
| Error, (in SumaPuntos) El punto p=[2, 0] no es un punto de la curva |
| > | SumaPuntos(1,-2,5,[1,0],[2,0],true); |
| Error, (in SumaPuntos) El punto q=[2, 0] no es un punto de la curva |
| > |
CurvasElipt[TablaSumas] - compute the addition of all the points of an Elliptic Curve
TablaSumas(a, b, n)
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
These are some examples of the use of the function TablaSumas(..) :
| > | TablaSumas(-1,3,5); |
 |
(14.9.4.1) |
| > | TablaSumas(1,-2,5); |
 |
(14.9.4.2) |
| > | TablaSumas(-1,3,7); |
 |
(14.9.4.3) |
| > | TablaSumas(0,-2,7); |
 |
(14.9.4.4) |
| > | TablaSumas(-4,2,11); |
 |
(14.9.4.5) |
| > | TablaSumas(-4,2,7); |
 |
(14.9.4.6) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | TablaSumas(3,1,2); |
| Error, (in TablaSumas) El n introducido debe ser distinto de 2 y de 3 |
| > | TablaSumas(5,1,3); |
| Error, (in TablaSumas) El n introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | TablaSumas(3,1,4); |
| Error, invalid input: TablaSumas expects its 3rd argument, n, to be of type prime, but received 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | TablaSumas(3,1,5); |
| Error, (in TablaSumas) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
CurvasElipt[LogaritmoPunto] - Discrete logarithm for Elliptic Curves
CurvasElipt[MúltiploPunto] - Multipy an Elliptic Curve's point by a number
LogaritmoPunto(a, b, n, P, Q)
MúltiploPunto(a, b, n, k, P)
Parameters
a, b |
- |
positive integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denotes the field ℤn |
k |
- |
integer |
P, Q |
- |
points of the elliptic curve |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
A point can be multiplied with MúltiploPunto function, and after that we can discover by which number was multiplied the point with LogaritmoPunto function:
| > | MúltiploPunto(-1,188,751,203,[565,194]); |
| (14.10.4.1) |
| > | LogaritmoPunto(-1,188,751,[565,194],%); |
| (14.10.4.2) |
| > | MúltiploPunto(-2,50,14831,12345,[14619,6880]); |
| (14.10.4.3) |
| > | LogaritmoPunto(-2,50,14831,[14619,6880],%); |
| (14.10.4.4) |
Now it is shown the list of points of the curve y2 = x3-2 in ℤ7:
| > | ListarPuntos(0,-2,7); |
| (14.10.4.5) |
Then the point [3,2] is multiplied by the numbers in 0..6 range:
| > | for i from 0 to 7-1 do
'i'=i, MúltiploPunto(0,-2,7,i,[3,2]); od; |
| (14.10.4.6) |
| > | Lista:=[]:
for i from 0 to 7-1 do Lista:=[op(Lista),MúltiploPunto(0,-2,7,i,[3,2])]; od: |
After that, it can be tested with LogaritmoPunto function that the previous products are rigth:
| > | for x in Lista do
print(`El logaritmo del punto `, x, `en base `, [3,2], `es `, LogaritmoPunto(0,-2,7,[3,2],x)); od; |
| (14.10.4.7) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | LogaritmoPunto(3,1,2,[0,1],[1,0]); |
| Error, (in LogaritmoPunto) El 'n' introducido debe ser distinto de 2 y de 3 |
| > | LogaritmoPunto(5,1,3,[0,1],[1,0]); |
| Error, (in LogaritmoPunto) El 'n' introducido debe ser distinto de 2 y de 3 |
| > | MúltiploPunto(3,1,2,7,[1,0]); |
| Error, (in MúltiploPunto) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | MúltiploPunto(5,1,3,7,[1,0]); |
| Error, (in MúltiploPunto) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | LogaritmoPunto(3,1,4,[0,1],[1,0]); |
| Error, invalid input: LogaritmoPunto expects its 3rd argument, n, to be of type prime, but received 4 |
| > | MúltiploPunto(3,1,4,7,[1,0]); |
| Error, invalid input: MúltiploPunto expects its 3rd argument, n, to be of type prime, but received 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | LogaritmoPunto(3,1,5,[0,1],[1,0]); |
| Error, (in LogaritmoPunto) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
| > | MúltiploPunto(3,1,5,7,[1,0]); |
| Error, (in MúltiploPunto) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
When the points do not belong to the elliptic curve, the function returns an error message:
| > | LogaritmoPunto(-1,3,5,[0,1],[1,0]); |
| Error, (in LogaritmoPunto) El punto p=[0, 1] no es un punto de la curva |
| > | LogaritmoPunto(-1,3,5,[2,2],[1,0]); |
| Error, (in LogaritmoPunto) El punto q=[1, 0] no es un punto de la curva |
| > | MúltiploPunto(-1,3,5,7,[1,0]); |
| Error, (in MúltiploPunto) El punto p=[1, 0] no es un punto de la curva |
When p is infinity, you can not compute the Discrete Logarithm for elliptic curves and the function returns an error message:
| > | LogaritmoPunto(-1,3,5,infinity,[2,2]); |
| Error, (in LogaritmoPunto) No se puede calcular el valor de k cuando p es infinito |
If it does not exist a k number such that q ≡ k · p, the function returns an error message:
| > | LogaritmoPunto(1,-2,5,[1,0],[4,1]); |
| Error, (in LogaritmoPunto) No se ha podido encontrar un valor para k |
The point infinity can not be multiplied by a negative number. In this case the function returns an error message:
| > | MúltiploPunto(-1,3,5,-5,infinity); |
| Error, (in CurvasElipt[SumaPuntosAUX]) El argumento 'p' debe ser una lista de 2 enteros o infinito. Se ha recibido [infinity[1], 4*infinity[2]] |
CurvasElipt[Koblitz] - Equivalent point in an Elliptic Curve for a symbol
Koblitz(a, b, n, m, A, k)
Parameters
a, b |
- |
integers |
n |
- |
prime |
m, A |
- |
strings |
k |
- |
positive integer |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
This function returns a point for each symbol:
| > | for x in "HOLA" do
Koblitz(-1,188,751,x,castellano,6); od; |
| (14.11.4.1) |
| > | Koblitz(-1,188,751,"A",castellano,6); |
| (14.11.4.2) |
| > | Koblitz(-1,188,751,"D",castellano,6); |
| (14.11.4.3) |
| > | Koblitz(-1,188,751,"I",castellano,6); |
| (14.11.4.4) |
| > | Koblitz(-1,188,751,"O",castellano,6); |
| (14.11.4.5) |
| > | Koblitz(-1,188,751,"S",castellano,6); |
| (14.11.4.6) |
If it receives more than a symbol, it returns the same point:
| > | Koblitz(-1,188,751,"HOLA",castellano,6); |
| (14.11.4.7) |
| > | Koblitz(-1,188,751,"ADIOS",castellano,6); |
| (14.11.4.8) |
| > | Koblitz(-1,188,751,"Mensaje de prueba",castellano,6); |
| (14.11.4.9) |
When the function can not find a point which encodes a symbol, it returns an error message:
| > | Koblitz(-1,3,5,"A","ABC",1); |
| Error, (in Koblitz) No se ha encontrado un punto que cifre el valor numérico del mensaje m = 'A' |
| > | Koblitz(-2,50,14831,"s", castellano,6); |
| Error, (in Koblitz) No se ha encontrado un punto que cifre el valor numérico del mensaje m = 's' |
CurvasElipt[PuntoTexto] - Symbol associated to a Point of an Elliptic Curve
CurvasElipt[TextoPunto] - Points of an Elliptic Curve associated to a string (plaintext)
PuntoTexto(a, b, n, P, A, k)
TextoPunto(a, b, n, men, A, k)
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
P |
- |
list of positive integer lists |
men, A |
- |
strings |
k |
- |
positive integer |
| > | restart;
libname:= libname,".": with(CurvasElipt): |
| > | TextoPunto(0,-1,53,"AB","ABC",10); |
| (14.12.4.1) |
| > | PuntoTexto(0,-1,53,%,"ABC",10); |
| (14.12.4.2) |
Assigment of points for the variable castellano symbols for the elliptic curve y2 = x3 -2x + 50 in ℤ 14831:
| > | ejemplo1:=TextoPunto(-2,50,14831,castellano,castellano,10); |
| (14.12.4.3) |
| > | PuntoTexto(-2,50,14831,ejemplo1,castellano,10); |
| (14.12.4.4) |
| > | ejemplo2:=TextoPunto(-2,50,14831,"castellano",castellano,10); |
| (14.12.4.5) |
| > | PuntoTexto(-2,50,14831,ejemplo2,castellano,10); |
| (14.12.4.6) |
Assigment of points for the variable castellano symbols for the elliptic curve y2 = x3 -3010x + 2005 in ℤ 123456789059:
| > | ejemplo3:=TextoPunto(3101,2005,123456789059,castellano,castellano,17); |
| (14.12.4.7) |
| > | PuntoTexto(3101,2005,123456789059,ejemplo3,castellano,17); |
| (14.12.4.8) |
Now it is used a normal message:
| > | ejemplo4:=TextoPunto(-2,50,14831,"Esto es un ejemplo de TextoPunto.¡A ver qué pasa!",castellano,10); |
| (14.12.4.9) |
| > | PuntoTexto(-2,50,14831,ejemplo4,castellano,10); |
| (14.12.4.10) |
| > | ejemplo5:=TextoPunto(3101,2005,123456789059,"Esto es un ejemplo de TextoPunto.¡A ver qué pasa!",castellano,17); |
| (14.12.4.11) |
| > | PuntoTexto(3101,2005,123456789059,ejemplo5,castellano,17); |
| (14.12.4.12) |
If k is small, he function fails to find a point and it returns an error message:
| > | TextoPunto(0,-1,53,"ABC","ABC",3); |
| Error, (in CurvasElipt[Koblitz]) No se ha encontrado un punto que cifre el valor numérico del mensaje m = 'C' |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | PuntoTexto(3,1,2,[[1,0]],"ABC",10); |
| Error, (in PuntoTexto) El n introducido debe ser distinto de 2 y de 3 |
| > | PuntoTexto(5,1,3,[[1,0]],"ABC",10); |
| Error, (in PuntoTexto) El n introducido debe ser distinto de 2 y de 3 |
| > | TextoPunto(3,1,2,"ABC","ABC",10); |
| Error, (in TextoPunto) El n introducido debe ser distinto de 2 y de 3 |
| > | TextoPunto(5,1,3,"ABC","ABC",10); |
| Error, (in TextoPunto) El n introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | PuntoTexto(3,1,4,[[1,0]],"ABC",10); |
| Error, invalid input: PuntoTexto expects its 3rd argument, n, to be of type prime, but received 4 |
| > | TextoPunto(3,1,4,"ABC","ABC",10); |
| Error, invalid input: TextoPunto expects its 3rd argument, n, to be of type prime, but received 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | PuntoTexto(3,1,5,[[1,0]],"ABC",10); |
| Error, (in PuntoTexto) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
| > | TextoPunto(3,1,5,"ABC","ABC",10); |
| Error, (in TextoPunto) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
When the n in ℤn is proportionally small to k, the function returns an error message:
| > | PuntoTexto(-1,3,5,[[1,0]],"ABC",10); |
| Error, (in PuntoTexto) El valor de n = 5 es pequeño para el tamaño de k introducido |
| > | TextoPunto(-1,3,5,"ABC","ABC",10); |
| Error, (in TextoPunto) El valor de n = 5 es pequeño para el tamaño de k introducido |
When you use a symbol that does not belong to the alphabet, it returns an error message:
| > | TextoPunto(0,-1,53,"«HOLA»",castellano,10); |
| Error, (in TextoPunto) El elemento '«' no pertenece al alfabeto |
CurvasElipt[GeneraClaveCE] - Key for Elliptic Curve Cryptosystem
GeneraClaveCE(a, b, n, base, k, 'priv')
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
base |
- |
list of two integers |
k |
- |
integer |
priv |
- |
evaln (can be evaluated to a name) |
| > | libname:= libname,".": with(CurvasElipt): |
If the n value is small, the function returns a warning message with the key:
| > | GeneraClaveCE(-1,3,5,[2,3],1,privCE1); |
| (14.13.4.1) |
| > | privCE1; |
| (14.13.4.2) |
| > | GeneraClaveCE(-1,3,5,[2,3],1,privCE2); |
| (14.13.4.3) |
| > | privCE2; |
| (14.13.4.4) |
These examples show a warning message because their length is not safe enough:
| > | GeneraClaveCE(-1,188,751,[565,194],1,privCE3); |
| (14.13.4.5) |
| > | privCE3; |
| (14.13.4.6) |
| > | GeneraClaveCE(-1,188,751,[565,194],2,privCE4); |
| (14.13.4.7) |
| > | privCE4; |
| (14.13.4.8) |
If the lenght of the key is greater than or equal to 3, it will be considered safe:
| > | GeneraClaveCE(-1,188,751,[565,194],3,privCE5); |
| (14.13.4.9) |
| > | privCE5; |
| (14.13.4.10) |
| > | GeneraClaveCE(-2,50,14831,[14619,6880],10,privCE6); |
| (14.13.4.11) |
| > | privCE6; |
| (14.13.4.12) |
| > | clave7:=GeneraClaveCE(3101,2005,123456789059,[100098,15890596801],10,privCE7); |
| (14.13.4.13) |
| > | privCE7; |
| (14.13.4.14) |
That is the Q = j · base mod p comprobation for "clave7" example, where Q is the public key:
| > | pública:=MúltiploPunto(3101,2005,123456789059,privCE7[1],clave7[2]); |
| (14.13.4.15) |
| > | is(pública = clave7[1]); |
| (14.13.4.16) |
Real case P-192 curve with a 10 digits lenght random number:
| > | ap192:=-3: bp192:=2455155546008943817740293915197451784769108058161191238065:
np192:=6277101735386680763835789423207666416083908700390324961279: Bp192:=[602046282375688656758213480587526111916698976636884684818,174050332293622031404857552280219410364023488927386650641]: #P-192 Curve |
| > | GeneraClaveCE(ap192,bp192,np192,Bp192,10,privP192); |
| (14.13.4.17) |
| > | privP192; |
| (14.13.4.18) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | GeneraClaveCE(3,1,2,[2,3],5,privCErr1); |
| Error, (in GeneraClaveCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | GeneraClaveCE(5,1,3,[2,3],5,privCErr2); |
| Error, (in GeneraClaveCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | GeneraClaveCE(3,1,4,[2,3],5,privCErr3); |
| Error, invalid input: GeneraClaveCE expects its 3rd argument, n, to be of type prime, but received 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | GeneraClaveCE(3,1,5,[2,3],5,privCErr4); |
| Error, (in GeneraClaveCE) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
When the point base does not belong to the elliptic curve, the function returns an error message:
| > | GeneraClaveCE(-1,3,5,[0,4],2,privCErr5); |
| Error, (in GeneraClaveCE) El punto base=[0, 4] no es un punto de la curva |
CurvasElipt[CifrarCE] - Encrypt messages with Elliptic Curve Cryptosystem
CurvasElipt[DescifrarCE] - Decrypt messages with Elliptic Curve Cryptosystem
Calling Sequence
CifrarCE(a, b, n, men, A, clavePub, miProb)
CifrarCE(a, b, n, men, A, clavePub)
DescifrarCE(a, b, n, cripto, A, clavePriv, miProb)
DescifrarCE(a, b, n, cripto, A, clavePriv)
Parameters
a, b |
- |
integers which are the coefficients of the elliptic curve |
n |
- |
prime, n ≠ 2, 3, which denote the field ℤn |
men, A |
- |
strings |
cripto |
- |
list of positive integer lists |
clavePub |
- |
list of two points of the Elliptic Curve |
clavePriv |
- |
list of an integer and a point of the Elliptic Curve |
miProb |
- |
(optional) float |
Description
Examples
| > | restart;
libname:=libname,".": with(CurvasElipt): |
The next example shows the use of the function:
| > | pública:=GeneraClaveCE(-2,50,14831,[14619, 6880],5,privada); |
| (14.14.4.1) |
| > | privada; |
| (14.14.4.2) |
| > | ejemplo:=CifrarCE(-2,50,14831,"La clave de tu operación es 1234",castellano,pública); |
| (14.14.4.3) |
| > | DescifrarCE(-2,50,14831,ejemplo,castellano,privada); |
| (14.14.4.4) |
Next example is a practical one:
First of all, Alicia (an user) creates her keys in order to send an receive messages. She uses the Elliptic Curve y2 = x3 -2x + 50 in ℤ14831 :
| > | clavePúblicaA:=GeneraClaveCE(-2,50,14831,[14619, 6880],5,privA); |
| (14.14.4.5) |
Alicia's private key will be:
| > | privA; |
| (14.14.4.6) |
Then Bob (another user) creates his keys with the same goal:
| > | clavePúblicaB:=GeneraClaveCE(-2,50,14831,[14619, 6880],5,privB); |
| (14.14.4.7) |
Bob's private key will be:
| > | privB; |
| (14.14.4.8) |
Then, Bob wants to send the next message to Alicia:
| > | mensaje:="¡Hola! ¿Qué tal? Estoy realizando una prueba del criptosistema de ElGamal."; |
| (14.14.4.9) |
So Bob has to encrypt the message with Alicia's public key and send the cryptogram to her:
| > | criptoB:=CifrarCE(-2,50,14831,mensaje,castellano,clavePúblicaA); |
| (14.14.4.10) |
When Alicia receives the encrypted message, she has to decrypt it with her private key:
| > | DescifrarCE(-2,50,14831,criptoB,castellano,privA); |
| (14.14.4.11) |
| > | is(%=mensaje); |
| (14.14.4.12) |
We are going to try when Alicia sends the next message to Bob:
| > | mensaje2:="Este es un mensaje en respuesta a Bob. Podrá leerlo cuando lo desencripte con su clave privada ;-)"; |
| (14.14.4.13) |
Then, Alicia encrypts her message with Bob's public key and sends the cryptogram to him:
| > | criptoA:=CifrarCE(-2,50,14831,mensaje2,castellano,clavePúblicaB); |
| (14.14.4.14) |
When Bob receives the cryptogram, he has to decrypt it with his private key in order to get the original message:
| > | DescifrarCE(-2,50,14831,criptoA,castellano,privB); |
| (14.14.4.15) |
| > | is(%=mensaje2); |
| (14.14.4.16) |
It is possible to chage the succes probability which is set to 0.9 by default. Notice that the cryptogram is different:
| > | criptoC:=CifrarCE(-2,50,14831,mensaje2,castellano,clavePúblicaB,0.95); |
| (14.14.4.17) |
| > | DescifrarCE(-2,50,14831,criptoC,castellano,privB,0.95); |
| (14.14.4.18) |
When the n in ℤn is 2 or 3, the function returns an error message:
| > | CifrarCE(3,1,2,mensaje,castellano,clavePúblicaA); |
| Error, (in CifrarCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | DescifrarCE(3,1,2,criptoA,castellano,privA); |
| Error, (in DescifrarCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | CifrarCE(5,1,3,mensaje,castellano,clavePúblicaA); |
| Error, (in CifrarCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
| > | DescifrarCE(5,1,3,criptoA,castellano,privA); |
| Error, (in DescifrarCE) El valor de 'n' introducido debe ser distinto de 2 y de 3 |
When the n in ℤn is not a prime number, the function returns an error message:
| > | CifrarCE(3,1,4,mensaje,castellano,clavePúblicaA); |
| Error, invalid input: CifrarCE expects its 3rd argument, n, to be of type prime, but received 4 |
| > | DescifrarCE(3,1,4,criptoA,castellano,privA); |
| Error, invalid input: DescifrarCE expects its 3rd argument, n, to be of type prime, but received 4 |
When the parameters a and b do not define an elliptic curve in ℤn, the function returns an error message:
| > | CifrarCE(3,1,5,mensaje,castellano,clavePúblicaA); |
| Error, (in CifrarCE) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
| > | DescifrarCE(3,1,5,criptoA,castellano,privA); |
| Error, (in DescifrarCE) La cúbica introducida no es curva elíptica, pues tiene raíces múltiples en Z5 |
The probability value has to be between 0 and 1. Otherwise the function returns an error message:
| > | CifrarCE(-2,50,14831,mensaje,castellano,clavePúblicaA,1.3); |
| Error, (in CifrarCE) La probabilidad introducida debe ser un valor entre 0 y 1. Se introdujo: 1.3 |
| > | DescifrarCE(-2,50,14831,criptoA,castellano,privA,1.3); |
| Error, (in DescifrarCE) La probabilidad introducida debe ser un valor entre 0 y 1. Se introdujo: 1.3 |
| > | CifrarCE(-2,50,14831,mensaje,castellano,clavePúblicaA,-0.5); |
| Error, (in CifrarCE) La probabilidad introducida debe ser un valor entre 0 y 1. Se introdujo: -.5 |
| > | DescifrarCE(-2,50,14831,criptoA,castellano,privA,-0.5); |
| Error, (in DescifrarCE) La probabilidad introducida debe ser un valor entre 0 y 1. Se introdujo: -.5 |
If the message contains a symbol which does not belong to the alphabet used, the function returns an error message:
| > | CifrarCE(-2,50,14831,"«HOLA»",castellano,clavePúblicaA); |
| Error, (in CifrarCE) El elemento '«' no pertenece al alfabeto |